E - E CodeForces - 1100E（拓扑排序 + 二分）

E - E CodeForces - 1100E

一个n个节点的有向图，节点标号从1到n，存在m条单向边。每条单向边有一个权值，代表翻转其方向所需的代价。求使图变成无环图，其中翻转的最大边权值最小的方案，以及该方案翻转的最大的边权。

Input 单组输入，第一行包含两个整数n和m(2≤n≤100 000,1≤m≤100 000) 接下来m行，每行3个整数，u_i ，v_i

，w_i （1<= u_i , v_i <= n, 1<= w_i <=

10^9），表示u到v有一条权值为w的道路。道路编号从1开始。没有自环。

Output 在第一行中输出两个整数，即要翻转的最大的边权，和需要反转道路数量k。k不需要是最小的。

在下一行输出k个由空格分隔的整数，表示需要翻转的道路编号

如果有许多解决方案，请打印其中任何一个。

Examples
Input
5 6
2 1 1
5 2 6
2 3 2
3 4 3
4 5 5
1 5 4
Output
2 2
1 3
Input
5 7
2 1 5
3 2 3
1 3 3
2 4 1
4 3 5
5 4 1
1 5 3
Output
3 3
3 4 7

思路

• 题意：给我一个有向带权值的图，这个图可能存在环，问所需改变的反转的边的最小权全是多少？
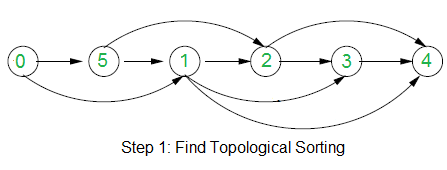
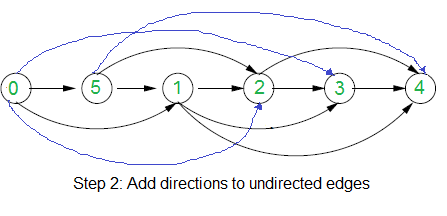
• 思路：首先用二分枚举，要反转边的最大边权的最小值mid，都一个所给的图中的边中 边权小于mid 把这个边视为双向边（不存在），然后在剩下的子图中 跑一边 拓扑排序， 看是否有环的存在，如果有的话让 让 l = mid + 1， 否则 r = mid - 1
• 链接
  
  
  
  

题解

#include<iostream>
#include<cmath>
#include<cstdio>
#include<queue>
#include<cstring>
#define int long long
#define inf 10000000000000
using namespace std;
int read(){
    int res=0;char ch=0;
    while (!isdigit(ch))ch=getchar();
    while (isdigit(ch))res=(res<<3)+(res<<1)+(ch^48),ch=getchar();
    return res;
}

const int N=1000100;
struct EDGE{
    int ver,nxt,dis,pre;
}edge[N];
int n,m,cnt,head[N],vis[N],d[N],ans[N],dfn[N],dfs_cnt;

void add(int u,int v,int t){
    edge[++cnt].ver=v;
    edge[cnt].nxt=head[u];
    edge[cnt].dis=t;
    edge[cnt].pre=u;
    head[u]=cnt;
}

queue<int>q;
bool check(int x){

    memset(d,0,sizeof(d));memset(vis,0,sizeof(vis));

    for (int i=1;i<=m;i++)if(edge[i].dis>x)d[edge[i].ver]++;

    for (int i=1;i<=n;i++)if (!d[i])q.push(i);

    while (!q.empty()){

        int u=q.front();q.pop();

        for (int i=head[u];i;i=edge[i].nxt)
        {
            if (edge[i].dis<=x)continue;

            int v=edge[i].ver;d[v]--;if (!d[v])q.push(v);
        }
    }

    for (int i=1;i<=n;i++)if (d[i])return 0;

    return 1;
}
void solute(int x){
    memset(d,0,sizeof(d));memset(vis,0,sizeof(vis));

    for (int i=1;i<=m;i++)if(edge[i].dis>x)d[edge[i].ver]++;
    for (int i=1;i<=n;i++)if (!d[i])q.push(i);

    while (!q.empty())
    {
        int u=q.front();q.pop();dfn[u]=++dfs_cnt;

        for (int i=head[u];i;i=edge[i].nxt)
        {
            if (edge[i].dis<=x)continue;
            int v=edge[i].ver;d[v]--;if (!d[v])q.push(v);
        }
    }

    for (int i=1;i<=m;i++){
        if (edge[i].dis<=x){
            int u=edge[i].pre,v = edge[i].ver;
            if (dfn[u]>dfn[v])ans[++cnt]=i;
        }
    }
}
signed main(){
    n=read();m=read();
    for (int i=1;i<=m;i++){
        int x=read(),y=read(),t=read();add(x,y,t);
    }
    int l=0,r=inf;
    while (l<r)
    {
        int mid=l+r>>1;
        if (check(mid))
            r=mid;
        else
            l=mid+1;
    }

    cnt=0;
    solute(r);
    printf("%lld %lld\n",r,cnt);
    for (int i=1;i<=cnt;i++){
        printf("%lld ",ans[i]);
    }
}