AdaBoost理解

AdaBoost是一种准确性很高的分类算法，它的原理是把K个弱分类器(弱分类器的意思是该分类器的准确性较低)，通过一定的组合(一般是线性加权进行组合)，组合成一个强的分类器，提高分类的准确性。

因此，要想使用AdaBoost，需要首先找几个弱的分类器出来，然后进行组合。这些弱分类器，其实可以自己指定，自己随意给出，但效果就不能保证。

要想通过AdaBoost得到一个准确性高的分类器，需要小心设计这些弱分类器。我自己理解，弱分类器可以采用最简单的形式，即二分法（二元分类器），取一个阈值v，某个特征小于v的是一类，该特征大于v的是另一类，至于这个阈值取多少合适，可以通过这个分类器的错误率(被错误分类的样本数除以总的样本数)来决定，若取阈值为v1得到的二元分类器的错误率为e1，而取阈值为v2的错误率e2，若e2<e1，说明v2更合适。还可以多取几个阈值，从中找出最佳的。《机器学习实战》解释了AdaBoost原理，但后面的代码让人不明白它到底在干啥。故自己理解之后，在此记录。

下面两篇文章可以帮助理解AdaBoost的算法过程和原理推导过程：

(1) AdaBoost算法过程： Adaboost算法原理分析和实例+代码

其中，sign(a1*h₁(x)+a2*h₂(X)+a3*h₃(x))，其中sign(*)表示取*的正负号，若*为正数，则sign(*)返回1，否则返回-1。而例子中：

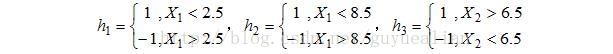
最后的分类器 f₃(x)=0.4236h₁(x) + 0.6496h₂(x)+0.9229h₃(x)，这里的h1(x)里面的x只是代表特征的意思，在这个例子中有x1,x2两个特征，因此，应该把两个特征都带进h1,h2,h3当中去。

例如，其中样本9 X9=(9,8),x1=9,x2=8,因此，h1(X)=-1,h2(X)=-1,h3(X)=1，于是f3(x)=0.4236*(-1)+0.6496*(-1)1+0.9229*1=-0.150299<0，因此f3(x)给出的分类结果为-1，分类结果是正确的。

(2) AdaBoost原理和推导： Adaboost 算法的原理与推导

Bagging和Boosting都是集成学习的一种实现方式，算是一种框架和思路，不是一个算法，因为它里面的弱分类器可以用决策树、svm、神经网络等各种算法进行组合。

另外，Bagging与Boosting的差别：https://www.cnblogs.com/liuwu265/p/4690486.html

bagging是从大数据集中随机抽样N次，形成N个不同的训练集，每个训练集得到一个弱分类器，再把这些弱分类器通过投票等方式进行组合，形成一个强分类器；而boosting是对同一个训练集迭代地进行训练，每次找出一个错误率最低的弱分类器，然后根据这个弱分类器的错误率计算更新每个样本的权重，这个权重将在下轮寻找错误率最低的弱分类器当中用到，因为错误率的计算方法就是把被弱分类器错分的样本的权重求和即为下一个弱分类器的错误率。详见：

https://blog.csdn.net/ruiyiin/article/details/77114072 （仔细看bagging和boosting的示意图）及

小象学院的“详解AdaBoost算法”（田野）这一课程，及小象学院“机器学习”课程的“12提升”的pdf文档中adaboost的举例 和  Adaboost 算法的原理与推导

https://blog.csdn.net/hero_boke/article/details/78991722