[总结]最近公共祖先(倍增求LCA)

目录

• 一、定义
• 二、LCA的实现流程
  • 1. 预处理
  • 2. 计算LCA
• 三、例题
  • 例1：P3379 【模板】最近公共祖先（LCA）
• 四、树上差分
  • 1. 边差分
  • 2. 点差分
  • 3. 例题

---

一、定义

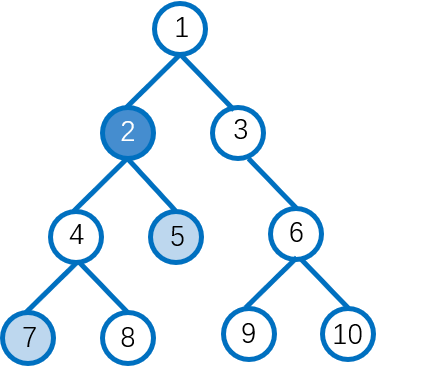
给定一颗有根树，若节点z既是节点x的祖先，也是节点y的祖先，则称z是x，y的公共祖先。在x，y的祖先中，深度最大的一个节点称为x，y的最近公共祖先(Least Common Ancestors)，记做LCA。

如图：LCA(5,7)=2；LCA(3,8)=1；LCA(6,10)=6。

二、LCA的实现流程

LCA一共有三种可以实现的方法：

1. 向上标记法
2. 倍增法
3. Tarjan算法(方法一的优化)

当然我们最熟悉不过的还是倍增法求LCA。

1. 预处理

在引入倍增优化之前，我们先来看看寻找两点LCA的朴素做法。

以寻找节点5，节点2的LCA为例：

首先求出每个点的深度，dep[7]=4，dep[5]=3。

我们先从深度大的节点7开始向上跳，直到深度和5一致，即跳到了节点4，此时这两个节点还没有到同一个点。

接下来我们继续让节点4和节点5向上跳，当他们跳到节点2的时候，由于跳到了相同节点，因此确定节点2是节点7，节点5的LCA。

显然，对于这样暴力的做法，速度慢的原因在于每一次只向上方跳一步，想要加快向上跳的速度，就需要采用倍增法进行优化。

我们设fa[x,k]表示x向上跳\(2^k\)的祖先节点，特别地，fa[x,0]就是x的父亲节点。

fa数组可以通过递推得出，x节点向上跳\(2^k\)步可以由x向上跳\(2^{k-1}\)步再向上跳\(2^{k-1}\)步推出。

递推方程：

\[fa[x][i+1]=fa[fa[x][i]][i];
\]

或者

\[fa[x][i]=fa[fa[x][i-1]][i-1];
\]

fa数组可以在遍历的时候求出，该预处理操作的总复杂度为\(O(NlogN)\)。

下面给出预处理的模板：

inline void Deal_first(int u,int fath){
	dep[u]=dep[fath]+1;
	fa[u][0]=fath;
	for(int i=0;i<20;i++) fa[u][i+1]=fa[fa[u][i]][i];//递推过程
	for(int e=first[u];e;e=next[e]){
		int v=go[e];
		if(v==fath) continue;
		Deal_first(v,u);
	}
}

2. 计算LCA

借助倍增优化计算x，y的LCA共需要跳logn步，因此时间复杂度为\(O(logN)\)。

我们首先需要将深度大的节点向上跳，直到两个节点深度相同，设dep[ ]表示每个节点的深度，若\(dep[x]\leq dep[y]\)，我们交换节点x，节点y(swap(x,y))使得节点x深度最大，此时我们将x向上调整到与y同一深度。操作完成后判断节点x是否等于节点y，如果相等，则说明LCA(x,y)=y，即x，y在一条链上，我们在此返回y即可。

当x，y跳到同一层后，我们利用二进制拆分思想，依次向上跳\(2^{logn},2^{logn-1},...,2^2,2^1,2^0\)步，同时让x，y向上调整并保证他们跳\(2^k\)步的父节点不相等(两个节点不相遇)。

循环结束后，x的父节点fa[x][0]就是节点x，y的LCA。

下面给出求LCA的模板：

int LCA(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);//减少代码长度，为了方便我们总让x先跳
	for(int i=20;i>=0;i--){//必须倒序循环，要证明正确性很简单，这里就不给具体证明过程了
		if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];
	}
	if(x==y) return y;
	for(int i=20;i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i];y=fa[y][i];
		}
	}
	return fa[x][0];
}

---

三、例题

例1：P3379 【模板】最近公共祖先（LCA）

Code：

#include<bits/stdc++.h>
#define re register
using namespace std;
int first[1000010],next[1000010],go[1000010],tot;
int dep[1000010],fa[1000010][22];
inline void read(int &x){
	x=0;int flag=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-') flag=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	x=x*flag;
}
inline void add_edge(int u,int v){
	next[++tot]=first[u];
	first[u]=tot;
	go[tot]=v;
}
inline void Deal_first(int pre,int u){
	dep[u]=dep[pre]+1;
	fa[u][0]=pre;
	for(re int i=0;i<20;i++) fa[u][i+1]=fa[fa[u][i]][i];
	for(re int e=first[u];e;e=next[e]){
		int v=go[e];
		if(v==pre) continue;
		Deal_first(u,v);
	}
}
int LCA(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(re int i=20;i>=0;i--){
		if(dep[fa[x][i]]>=dep[y])
			x=fa[x][i];
		if(x==y) return y;
	}
	for(re int i=20;i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i];
			y=fa[y][i];
		}
	}
	return fa[x][0];
}
int main()
{
	int m,n,s,u,v;
	read(n),read(m),read(s);
	for(re int i=1;i<=n-1;i++){
		read(u),read(v);
		add_edge(u,v);add_edge(v,u);
	}
	Deal_first(0,s);
	int a,b;
	for(re int i=1;i<=m;i++){
		read(a),read(b);
		printf("%d\n",LCA(a,b));
	}
	return 0;
}

---

四、树上差分

差分思想我们已经在树状数组的那篇文章中(原文链接)提及，差分与树上差分的区别在于：差分在序列上操作，而树上差分则在一棵树上进行操作。

树上差分可以解决树上一段连续区间的权值更改问题。

分类：树上差分分为点差分和边差分两类。

1. 边差分

边差分修改一段连续区间的边权。

以节点x到节点y的最短路径上的边权都加1为例：

其中，fa[ ]数组表示任意节点的父节点。

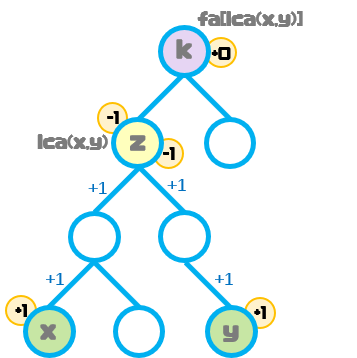
我们设数组p[ ]表示每个节点的点权，因此得到p[x]+=1，p[y]+=1。

由于x，y的最近公共祖先节点z的点权不受边权的改变而改变，因此可以得出p[z]-=2，即x，y的贡献均到节点z结束。

这样节点z及以上节点都能保证正确性。

最终的操作为：p[x]++; p[y]++; p[lca(x,y)]-=2;

2. 点差分

点差分修改一段连续区间的点权。

我们同样以节点x到节点y的最短路径上的点权都加1为例：

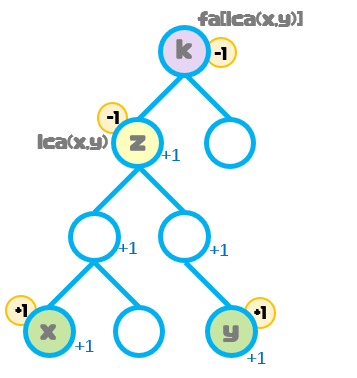
我们不难发现，点差分中节点x，节点y的差分数组是没有变化的，仍为p[x]+=1，p[y]+=1。

由于修改的是点权，此时的节点z也会加一个点权，如果我们按照边差分的方式处理节点z，那么就相当于节点z没有被影响到，也就是说点z的点权没有变化。

由于点z子树内的节点会对它贡献两次答案，因此我们只在节点z的差分数组里减1，就可以只一个贡献答案。

此时我们的操作还没有结束，因为点z的差分数组中仍+1，即z会对它的祖先节点产生影响。

我们只需要在点z的父节点k的差分数组中减去1就能消除影响。

最终的操作为：p[x]++; p[y]++; p[lca(x,y)]--;p[fa[lca(x,y)]]--;

3. 例题

P3128 [USACO15DEC]最大流Max Flow

点差分的模板题。

Code：

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#define N 100010
#define INF 0x7fffffff
using namespace std;
int n,m,tot,ans=-INF;
int fa[N<<2][22],dep[N<<2],p[N<<1];
int first[N<<1],nxt[N<<1],go[N<<1];
inline void add_edge(int u,int v){
	nxt[++tot]=first[u];
	first[u]=tot;
	go[tot]=v;
}
void Deal_first(int u,int fath){
	dep[u]=dep[fath]+1;
	fa[u][0]=fath;
	for(int i=0;i<20;i++)
		fa[u][i+1]=fa[fa[u][i]][i];
	for(int e=first[u];e;e=nxt[e]){
		int v=go[e];
		if(v==fath) continue;
		Deal_first(v,u);
	}
}
int LCA(int x,int y)
{
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=20;i>=0;i--){
		if(dep[fa[x][i]]>=dep[y])
			x=fa[x][i];
		if(x==y) return x;
	}
	for(int i=20;i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i];
			y=fa[y][i];
		}
	}
	return fa[x][0];
}
void DFS_get_path(int u,int fath){
	for(int e=first[u];e;e=nxt[e]){
		int v=go[e];
		if(v==fath) continue;
		DFS_get_path(v,u);
		p[u]+=p[v];//该点影响由自己以及子树中的节点贡献
	}
	ans=max(ans,p[u]);//求最大压力
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		add_edge(u,v);
		add_edge(v,u);
	}
	Deal_first(1,0);
	for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		int lca=LCA(x,y);
		p[x]++;p[y]++;//树上差分的核心
		p[lca]--;
		p[fa[lca][0]]--;
	}
	DFS_get_path(1,0);
	printf("%d",ans);
	return 0;
}

---