高斯朴素贝叶斯（Gaussian Naive Bayes）原理与实现——垃圾邮件识别实战

朴素贝叶斯（Naive Bayes）：

根据贝叶斯定理和朴素假设提出的朴素贝叶斯模型。

贝叶斯定理：

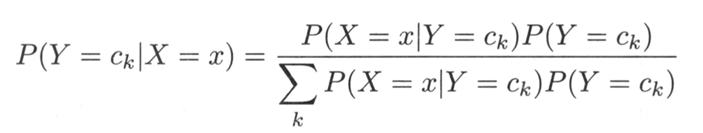
朴素假设（特征条件独立性假设）：

代入可知朴素贝叶斯模型计算公式：

因为朴素贝叶斯是用来分类任务，因此：

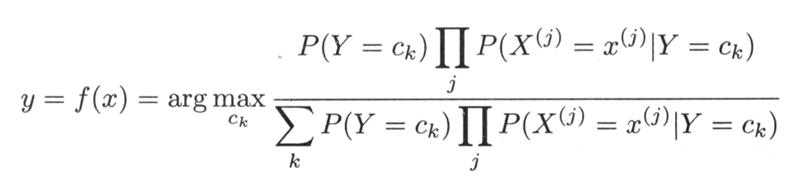
化简可知：

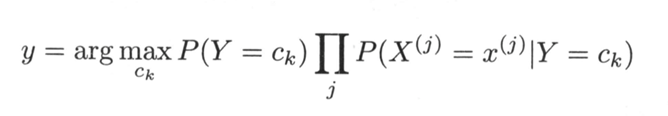
朴素贝叶斯模型除了上式所描述的以外，有三种常用的模型：

1、高斯朴素贝叶斯

2、多项式朴素贝叶斯

3、伯努利朴素贝叶斯

本篇主要是实现高斯朴素贝叶斯，因为它是最常用的一种模型。

高斯朴素贝叶斯：

适用于连续变量，其假定各个特征 _ 在各个类别下是服从正态分布的，算法内部使用正态分布的概率密度函数来计算概率。

_：在类别为的样本中，特征_的均值。

_：在类别为的样本中，特征_的标准差。

高斯朴素贝叶斯代码实现：

注释：

1、var_smoothing和epsilon的目的是防止一些特征的方差为0的情况（比如在垃圾邮件识别的时候，使用词袋模型很容易出现方差为0）

2、计算联合概率时并不使用连乘，对概率取自然对数，乘法变加法，降低计算复杂度，使模型更稳定。

 1 import numpy as np
 2 import collections
 3 import math
 4 class GaussianNB(object):
 5     def __init__(self):
 6         self.mp = {} #把y值映射到0-n之间的整数
 7         self.n_class = None #类别数
 8         self.class_prior= None #先验概率P(Y)
 9         self.means = None #均值
10         self.vars = None  #方差
11         self.var_smoothing =1e-9 #平滑因子
12         self.epsilon = None #平滑值
13     def _get_class_prior(self,y):
14         cnt = collections.Counter(y)
15         self.n_class = 0
16         for k,v in cnt.items():
17             self.mp[k] = self.n_class
18             self.n_class+=1
19         self.class_prior = np.array([ v/len(y) for k,v in cnt.items()])
20         pass
21     def _get_means(self,xx,y):
22         new_y =np.array([self.mp[i] for i in y])
23         self.means = np.array([ xx[new_y==id].mean(axis=0) for id in range(self.n_class)])
24         # self.means shape: n_class * dims
25         pass
26     def _get_vars(self,xx,y):
27         new_y = np.array([self.mp[i] for i in y])
28         self.vars = np.array([xx[new_y == id].var(axis=0) for id in range(self.n_class)])
29         # self.vars shape: n_class * dims
30         pass
31     def fit(self,X,Y):
32         # X 必须是numpy的array; Y为list,对于X中每个样本的类别
33         self._get_class_prior(Y)
34         self._get_means(X,Y)
35         self._get_vars(X,Y)
36         self.epsilon = self.var_smoothing * self.vars.max() #选取特征中最大的方差作为平滑
37         self.vars = self.vars + self.epsilon #给所有方差加上平滑的值
38         pass
39     def _get_gaussian(self,x,u,var):
40         #计算在类别y下x的条件概率P(xj|y)的对数
41         #return math.log(1 / math.sqrt(2 * math.pi * var) * math.exp(-(x - u) ** 2 / (2 * var)))
42         return -(x - u) ** 2 / (2 * var) - math.log(math.sqrt(2 * math.pi * var))
43     def predict(self,x):
44         dims = len(x)
45         likelihoods = []
46         for id in range(self.n_class): #遍历每类yi，把每个特征的条件概率P(xj|yi)累加
47             likelihoods.append(np.sum([self._get_gaussian(x[j], self.means[id][j], self.vars[id][j]) for j in range(dims)]))
48         # 对先验概率取对数
49         log_class_prior = np.log(self.class_prior)
50         all_pros = log_class_prior + likelihoods
51         #all_pros = self.standardization(all_pros)
52         max_id = all_pros.argmax() #取概率最大的类别的下标
53         for k,v in self.mp.items(): #转换为可读的y值
54             if v== max_id:
55                 return k
56         pass
57     def standardization(self,x):
58         mu = np.mean(x)
59         sigma = np.std(x)
60         return (x - mu) / sigma
61
62 # nb = GaussianNB()
63 # xx = np.array([[1,2,3],[11,12,1],[2,1,4],[15,16,1],[8,6,6],[19,13,0]])
64 # y = ['min','max','min','max','min','max']
65 # nb.fit(xx,y)
66 # print(nb.predict(np.array([0,0,0])))

垃圾邮件识别实战：

数据集：Trec06C数据集

笔者获取的数据集是处理过的

处理方式：随机选取：5000封垃圾邮件和5000封正常邮件；

预处理提取邮件正文，去掉换行符、多余空格等UTF-8文本格式，每封邮件正文在文件中保存为一行文本其中前5000 条为垃圾邮件，后5000 条为正常邮件。

特征提取：使用词袋模型进行特征提取（特征维度33453）

模型训练：模型训练和验证将数据集随机切分为训练集和测试集（40%）；使用GaussianNB高斯贝叶斯进行训练。

实验结果：在测试集上准确率达到了97.95%，效果还是不错的

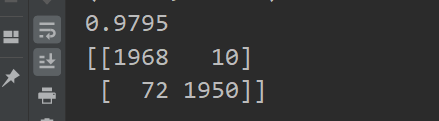
实验代码：

注释：代码跑起来比较慢，主要是因为预测的函数并不是将所有的句子一起预测，而是一句一句预测了。最近没啥空改这个，等下次需要的时候再更新吧。

 1 import numpy as np
 2 import jieba
 3 from sklearn.feature_extraction.text import CountVectorizer
 4 from sklearn import model_selection, metrics
 5 from GaussianNB import GaussianNB
 6 file_path = 'email.txt'
 7 file = open(file_path,encoding='utf-8')
 8 data = file.readlines()
 9 y = ['Spam']*5000+['Normal mail']*5000
10 split_data = []
11 for line in data:
12     split_data.append(' '.join(jieba.lcut(line)))
13 print(split_data[-1])
14 #仅保留长度至少为2个汉字的词
15 cv = CountVectorizer(token_pattern=r"(?u)\b\w\w+\b")
16 xx = cv.fit_transform(split_data).toarray()
17 print(xx.shape)
18
19 x_train, x_test, y_train, y_test =  model_selection.train_test_split(xx,y,test_size=0.4)
20 gnb = GaussianNB()
21 gnb.fit(x_train,y_train)
22 y_pre  =[]
23 for x in x_test:
24     y_pre.append(gnb.predict(x))
25 print(metrics.accuracy_score(y_test,y_pre))
26 print (metrics.confusion_matrix(y_test, y_pre))

参考资料：

1、《统计学习方法（第二版）》——李航

2、https://zhuanlan.zhihu.com/p/64498790