Note -「Suffix Automaton」SAM

Part. 1 基本信息

Part. 1-1 SAM 的构成。

SAM 由两个东西构成，一个是一个 DAWG，还有一棵外向树，叫 parent tree。

比如，给你一个字符串 \(S=\sf abbabb\)，它的 SAM 长成这样：

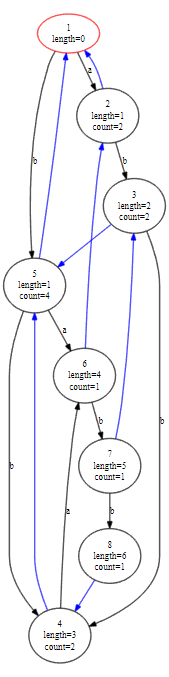
SAM 的 DAWG 大概可以理解为把字符串的所有后缀插入一个 Trie。当然如果你暴力插，点数为 \(\mathcal{O}(n^2)\)。

不过显然我们可以把一些重复的结点 rua 在一起，点数差不多就成了 \(\mathcal{O}(n)\)，还要带个 \(2\) 的常数。

然后，\(S\) 的子串都可以被 SAM 的 DAWG 上的某条路径表示，很显，对吧。

DAWG 的边就是上图中的黑边，蓝边就是 parent tree 的树边。

Part. 1-2 符号约定

我们称 \(S[l,r]\) 为字符串 \(S\) 的 \([l,r]\) 的子串，相信大家都懂，下标从 \(1\) 开始。

我们称一个集合 \(\text{endpos}(S[l,r])\) 为：对于字符串 \(S\)，\(S[l,r]\) 在 \(S\) 中出现的区间为 \([l_{1},r_{1}],\cdots,[l_{k},r_{k}]\)，\(\text{endpos}(S[l,r])=\{r_{1},\cdots,r_{k}\}\)。

对于两个子串 \(x,y\)，如果 \(\text{endpos}(x)=\text{endpos}(y)\)，则称 \(x,y\) 在同一个 \(\text{endpos}\) 等价类中。

显然在 DAWG 上，从根节点到一个结点 \(u\) 能组成的字符串的长度是不同的（不同的路径组成的字符串长度不一定等），我们称从根节点到一个结点 \(u\) 能组成的最长的一个字符串的长度为 \(\text{maxlen}(u)\)，最短的称为 \(\text{minlen}(u)\)。

Part. 2 需要知道的

Part. 2-1 \(\text{enspos}\) 的性质

引理 1：对于两个 \(S\) 的非空子串 \(x,y\)（不妨设 \(|x|<|y|\)），若 \(\text{endpos}(x)=\text{endpos}(y)\)，则 \(x\) 为 \(y\) 的一个真后缀。

Obviously。

引理 2：对于两个 \(S\) 的非空子串 \(x,y\)（不妨设 \(|x|\le|y|\)），则

\[\begin{cases}
\text{endpos}(x)\subseteq\text{endpos}(y),x\text{ is a suffix of } y, \\
\displaystyle\\
\text{endpos}(x)\cap\text{endpos}(y),\text{otherwise}
\end{cases}
\]

Obviously。

引理 3：在一个 \(\text{endpos}\) 等价类中，将类中的所有子串按长度非递增的顺序排序。每个子串都不会比它前一个子串长，与此同时每个子串也是它前一个子串的后缀。换句话说，对于同一等价类的任一两子串，较短者为较长者的后缀，且该等价类中的子串长度恰好覆盖整个区间 \([x,y]\)。

由引理 1，可知这些子串不会等长（对于两个串，较短串为较长串的真后缀），后面 obviously。

说得简单一点，把一个等价类里面最长的那个字符串拿出来，其他所有串都是该串的 suffix。

Part. 2-2 后缀链接 Link

后缀链接是在原串的 DAWG 上的点连出的边。后缀链接的链接遵循某种规则，且最后构成的是一棵树，我们把后缀链接连出来的树称为 Parent Tree，在后文我们将讲解这种规则。

我们先来看看一个串 \(S=\sf aababa\) 的 Parent Tree 长成副什么样子：

图是从 command_block 那里拿来的，可以沟通删除。（已经修正了原图的勘误）

为了说明方便，我们以一个任意的等价类来说明，我们称这个等价类中长度最大的串为 \(S_{\max}\)，同理有 \(S_{\min}\)。

考虑在 \(S_{\max}\) 前面加上一个字符，称为新串为 \(S_{\text{new}}\)，显然 \(S_{\text{new}}\) 一定不和 \(S_{\max}\) 在同一等价类里。

我们把上述 加字符 的操作看为分裂出儿子。有了这些，我们可以得出一些性质：

1. 设 Parent Tree 上的父亲为 \(f\)，儿子为 \(u\)，有 \(\text{minlen}(u)=\text{maxlen}(f)+1\)，显然。

2. 点数边数皆为 \(\mathcal{O}(n)\)，不考虑证明，背着。

3. 在 Parent Tree 上，一个结点的父亲一定是该结点的后缀，显然。

最后板子自己理解性背住吧，构造方法不想写了。

struct SuffixAutomaton
{
	int ID(char c)
	{
		return c-'a';
	}
	struct node
	{
		int len,link,ch[26];
	}nodes[3000010];
	int n,cntot,las,siz[3000010];
	char s[1000010];
	vector<int> e[3000010];
	void init(int len,char c[])
	{
		n=len;
		for(int i=1;i<=n;++i)	s[i]=c[i];
		nodes[0].len=las=cntot=0;
		nodes[0].link=-1;
	}
	void extend(char c)
	{
		int cur=++cntot,one=las,ano=0;
		nodes[cur].len=nodes[las].len+1;
		while(~one&&!nodes[one].ch[ID(c)])
		{
			nodes[one].ch[ID(c)]=cur;
			one=nodes[one].link;
		}
		if(one==-1)	nodes[cur].link=0;
		else
		{
			ano=nodes[one].ch[ID(c)];
			if(nodes[one].len+1==nodes[ano].len)	nodes[cur].link=ano;
			else
			{
				int clone=++cntot;
				nodes[clone].len=nodes[one].len+1;
				nodes[clone].link=nodes[ano].link;
				memcpy(nodes[clone].ch,nodes[ano].ch,sizeof(int)*26);
				while(~one&&nodes[one].ch[ID(c)]==ano)
				{
					nodes[one].ch[ID(c)]=clone;
					one=nodes[one].link;
				}
				nodes[ano].link=nodes[cur].link=clone;
			}
		}
		siz[las=cur]=1;
	}
	void pre()
	{
		for(int i=1;i<=n;++i)	extend(s[i]);
		for(int i=1;i<=cntot;++i)	e[nodes[i].link].push_back(i);
	}
	void dfs(int x)
	{
		for(int i=0;i<e[x].size();++i)
		{
			int y=e[x][i];
			dfs(y);
			siz[x]+=siz[y];
		}
		if(siz[x]^1)	ans=max(ans,siz[x]*nodes[x].len);
	}
}SAM;

代码中的 siz 是 \(\text{endpos}\) 集合大小。