Akima算法

测量数据的内插已有各种方法,如线性内插、多项式内插、样条函数插值等,但这里的Akima插值法具有独特的优点。

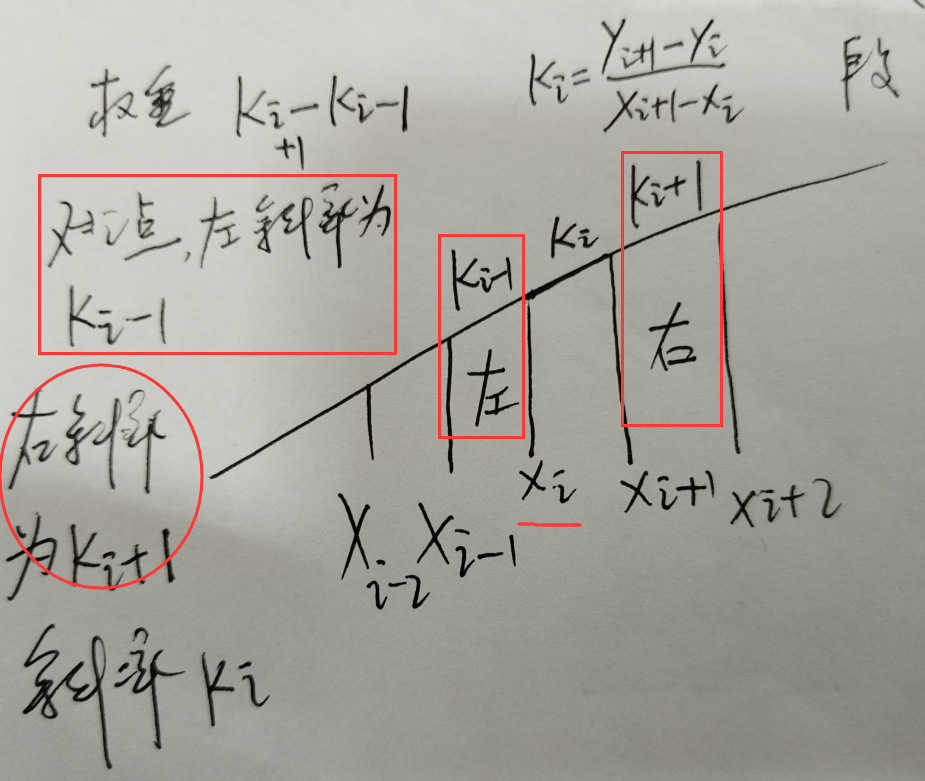
线性内插只顾及其附近两点的影响。

多项式内插时,低阶多项式由于参数较少,内插精度很低,而使用高阶多项式又会使解不稳定,出现“龙格”现象,即内插函数在插值点与实际数据符合得很好,而在插值点外出现较大的偏差。因此人们又在多项式的基础上发展了分片多项式,即样条函数。

样条函数既保持了多项式运算简单的特点,又避免了多项式阶数较高时数值不稳定的缺点,因而得到了广泛的应用。但在样条函数插值中,确定任何一个小区间上的多项式,都要考虑所有数据点对它的影响。这不仅扩大了误差传播的范围,还增加了不少工作量。有时只用内插点附近的几个数据点作为控制点来内插。

Aikma插值法和三次样条函数一样考虑了要素导数值的效应,因而得到的整个插值曲线是光滑的。三次样条函数插值法具有最小模、最佳最优逼近和收敛的特性,而Aikma插值法所得曲线比样条函数插值曲线更光顺,更自然。

https://blog.csdn.net/bluels01/article/details/43561131

Akima算法是一个插值算法，即对于一个已知（Xi，yi）的数据集，为了让曲线看起来平滑、自然，依据现有的数据点，通过插值，多出一些数据点的过程。

C++中的Akima算法

#include <iostream>
#include <vector>
#include <cmath>

// Akima插值函数
double akimaInterpolation(double x, const std::vector<double>& xData, const std::vector<double>& yData) {
int n = xData.size();

int index = 0;

// Find the interval index
for (int i = 0; i < n - 1; ++i) {
if (x >= xData[i] && x <= xData[i + 1]) {
index = i;
break;
}
}

// 计算斜率
std::vector<double> slopes(n - 1); //初始化n-1个默认值为0的元素
for (int i = 0; i < n - 1; ++i) {
double dx = xData[i + 1] - xData[i];
double dy = yData[i + 1] - yData[i];
slopes[i] = dy / dx; //计算每段之间的斜率
}

// 计算权重
std::vector<double> weights(n - 1); //初始化n-1个默认值为0的元素
for (int i = 2; i < n - 2; ++i) {
weights[i] = std::abs(slopes[i + 1] - slopes[i - 1]); //计算这些权重的目的是确定每个间隔附近的斜坡的“强度”。这些权重随后用于插值公式中，以确保插值曲线的平滑性和连续性。
}

// 计算插值
double dx = xData[index + 1] - xData[index];
double t = (x - xData[index]) / dx; //参数 t 表示区间内的归一化位置，取值范围为 0 到 1

//m0、m1、p0和p1是 A​​kima 插值公式中用于计算插值的系数
double m0 = slopes[index] * dx; //详见代码解析1
double m1 = slopes[index + 1] * dx;
double p0 = (3 * weights[index] - 2 * m0 - m1) / dx; //这里的3，2系数是怎么来的详见代码解析2
double p1 = (3 * weights[index + 1] - m0 - 2 * m1) / dx;
//interpolatedValue 这个公式用于计算最终插值结果，详见代码解析3
double interpolatedValue =
yData[index] * (1 - t) * (1 - t) * (1 + 2 * t) +
yData[index + 1] * t * t * (3 - 2 * t) +
p0 * t * (1 - t) * (1 - t) +
p1 * t * t * (t - 1);

return interpolatedValue;
}

int main() {
std::vector<double> xData = {1, 2, 3, 4, 5};
std::vector<double> yData = {1, 3, 2, 5, 4};

// 假设输入一个x=2.5,y输出多少？
double interpolatedValue = akimaInterpolation(2.5, xData, yData);
std::cout << "Interpolated value at x = 2.5: " << interpolatedValue << std::endl;

return 0;
}

解释一下上面的斜率和权重，斜率是通过相邻点之间 k=dy/dx 来计算。而权重是区间附近斜率对这个区间影响的权重，将点i的左侧斜率slopes[i - 1]和右侧斜率slopes[i + 1]相减得到，存在weights[i]里。权重随后用于插值公式中，以确保插值曲线的平滑性和连续性。

这里展开讲一下：
在 Akima 插值中，插值曲线是通过将分段三次曲线拟合到连续数据点之间的每个区间来构建的。这些三次曲线的斜率在确定插值曲线的形状和行为方面起着至关重要的作用。目标是确保曲线连续并遵循数据的总体趋势，同时避免过度振荡。

通过计算权重算法考虑了相邻区间之间斜率的变化。权重通过捕获数据的局部行为并影响插值过程中每个斜率的“强度”。较大的权重表示区域斜率变化明显，而较小的权重表示区域较平滑。

在执行插值时，将权重合并到插值公式中以调整相邻斜率的贡献。权重充当控制不同区间斜率之间平衡的系数。此调整有助于平滑插值曲线并减少由异常值或噪声数据点引起的突然变化。

代码解析1
m0、m1、p0和p1是 A​​kima 插值公式中用于计算插值的系数：

m0：此变量表示左相邻区间的调整斜率。将当前区间 (slopes[index]) 的斜率乘以区间宽度 ( dx)得到。

m1：此变量表示右相邻区间的调整斜率。将下一个区间 (slopes[index + 1]) 的斜率乘以区间的宽度 (dx)得到。

p0：此变量表示左相邻区间的调整权重。它是使用当前区间 ( weights[index]) 的权重、左侧区间的调整斜率 ( m0) 和右侧区间的调整斜率 (m1) 计算得到。由公式(3 * weights[index] - 2 * m0 - m1) / dx确定左相邻区间对插值的贡献。

p1：此变量表示右相邻区间的调整权重。它是使用下一个区间的权重 ( weights[index + 1])、左侧区间的调整斜率 (m0) 和右侧区间的调整斜率 (m1) 计算得到。由公式(3 * weights[index + 1] - m0 - 2 * m1) / dx确定右相邻区间对插值的贡献。

代码解析2
公式(3 * weights[index] - 2 * m0 - m1) / dx 和 (3 * weights[index + 1] - m0 - 2 * m1) / dx 是基于Akima插值方案推导出来的。
为了理解推导，让我们考虑 Akima 插值方案的一般形式：

y(x) = p0(x) * y0 + p1(x) * y1 + q0(x) * m0 + q1(x) * m1
在此等式中，y(x)表示特定坐标处的插值x。y0和y1是x两侧的数据点， m0和m1是与数据点关联的斜率。项p0(x)和p1(x)是数据点的权重系数，q0(x)和q1(x)是数据点关联的斜率的权重系数。
       为了确定p0(x)和p1(x)，Akima 拟合使用三次多项式来确保平滑性和连续性。这些权重系数由斜率的局部行为决定。

通过考虑Akima插值方案，我们可以推导出代码中使用的具体权重公式：

对于p0(x)：权重函数p0(x)决定了左邻域的贡献。在代码中，(3 * weights[index] - 2 * m0 - m1) / dx代表p0(x).
选择特定系数3、-2和1是为了平衡斜率的影响并确保间隔边界处的连续性。这些系数是通过数学分析和优化确定的。

对于p1(x)：权重函数p1(x)决定了右邻区间的贡献。在代码中，(3 * weights[index + 1] - m0 - 2 * m1) / dx代表p1(x).同样，选择系数3、-1和-2以实现插值曲线的连续性和平滑性。

导出这些公式中的特定系数是为了最大限度地减少插值误差并保持曲线的连续性。它们是通过数学分析和优化技术确定的，以确保生成的曲线与基础数据点紧密匹配。

代码解析3
　　yData[index] * (1 - t) * (1 - t) * (1 + 2 * t)：这一项代表左边数据点（yData [index]) 对插值的贡献。它乘以三次多项式“(1 - t) * (1 - t) * (1 + 2 * t)”，该多项式取决于参数“t”，范围从 0 到 1。多项式旨在确保左侧数据点的平滑过渡和适当加权。
　　yData[index + 1] * t * t * (3 - 2 * t)：此项表示右侧数据点 (yData[index + 1]) 对插值的贡献。它乘以三次多项式“t * t * (3 - 2 * t)”。与上面类似，这个多项式确保了右侧数据点的平滑过渡和适当加权。
       p0 * t * (1 - t) * (1 - t)：此项表示左侧相邻区间的调整权重 (p0) 对插值的贡献。它乘以三次多项式“t * (1 - t) * (1 - t)”。该多项式表示左侧相邻区间对插值的影响。
        p1 * t * t * (t - 1)：此项表示右相邻区间的调整权重 (p1) 对插值的贡献。它乘以三次多项式“t * t * (t - 1)”。该多项式表示右侧邻区间对插值的影响。
        该方程结合了相邻数据点的贡献及其相应的权重来计算最终的插值。参数 t 表示区间内的归一化位置，取值范围为 0 到 1。它决定了相邻数据点及其对应区间的相对权重。应用于数据点和权重的三次多项式确保插值曲线的平滑性和连续性。
把上面这些影响因素加一起就是插值点的函数值interpolatedValue了。

备注：以上资料主要来源于以下链接

https://blog.csdn.net/silent_dusbin/article/details/131316458?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-1-131316458-blog-125541966.235%5Ev43%5Epc_blog_bottom_relevance_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-1-131316458-blog-125541966.235%5Ev43%5Epc_blog_bottom_relevance_base3&utm_relevant_index=2