【HarmonyOS】详解低代码端云一体化开发之数据模型
【关键字】
元服务、低代码平台、端云一体化开发、数据模型、拖拽式UI
【1、写在前面】
上一篇中分享了关于低代码平台开发元服务的基本使用，有兴趣的可以看一下，文章地址如下：
https://developer.huawei.com/consumer/cn/forum/topic/0201120502584194043?fid=0101591351254000314
但是在上一篇中我们的数据都是在端侧配置的，这种方式肯定是无法满足我们的实际需求的，所以本篇将会使用一种全新的方式来为端侧应用接入数据——低代码平台数据模型。
【2、开通低代码平台】
数据模型是在AppGallery Connect控制台中创建的一种云侧的数据资源，在端侧绑定已经创建好的需要的数据模型，就可以实现端侧调用云侧数据展示的效果。
如果你想要使用云侧数据模型的能力，需要先申请加入白名单，在白名单通过之后还要在AppGallery Connect中开通低代码平台，完成以上两步之后才可以愉快的使用数据模型的能力，关于这两步操作的详细步骤可以参考以下说明文档：
申请加入白名单：
开通低代码平台：
【3、实战案例】
下面通过实现一个加载列表数据的功能来具体看一下如何使用数据模型。
3.1、端侧UI布局
首先，我们在端侧通过拖拽式开发UI界面，这里实现一个List列表，然后ListItem中先是左右布局：左侧Image图片、右侧文本，然后右侧文本是上下布局，高度各占50%，整体UI布局效果如下：
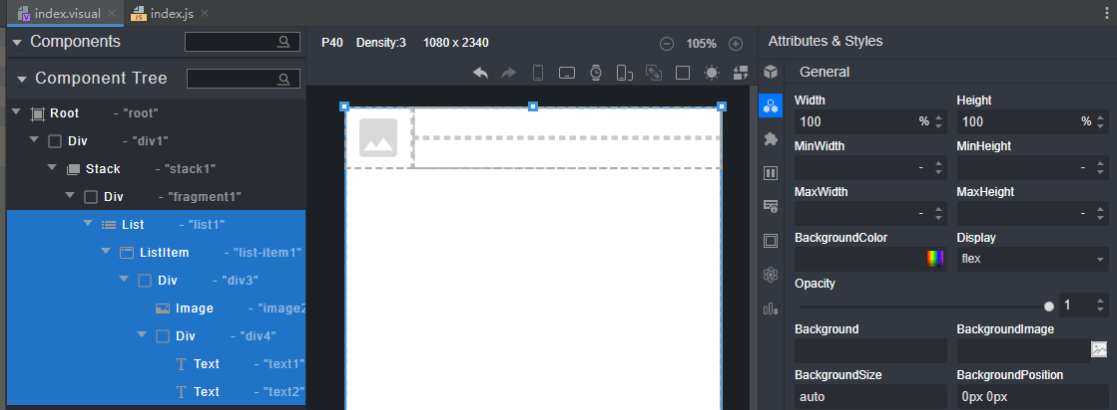
3.2、云侧数据模型
首先登录AppGallery Connect控制台，然后选择对应的项目，找到左侧导航栏中的“低代码平台”--->“数据模型”，如下图所示：
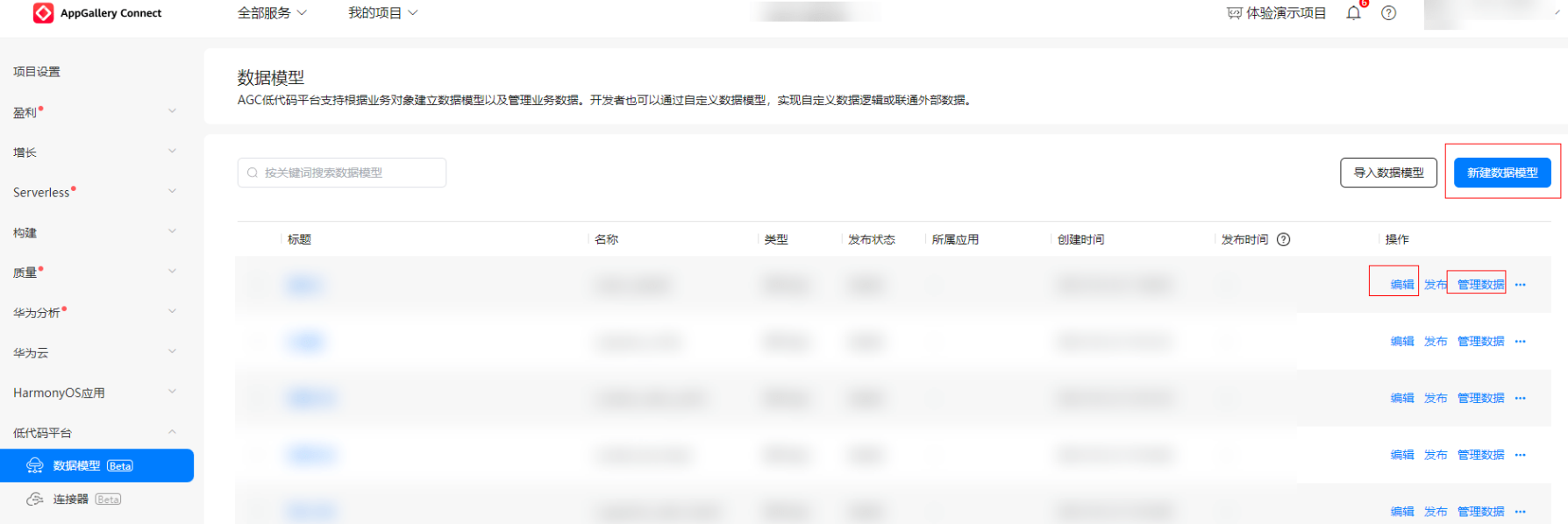
点击新建数据模型，在弹出的对话框中填写相应信息：
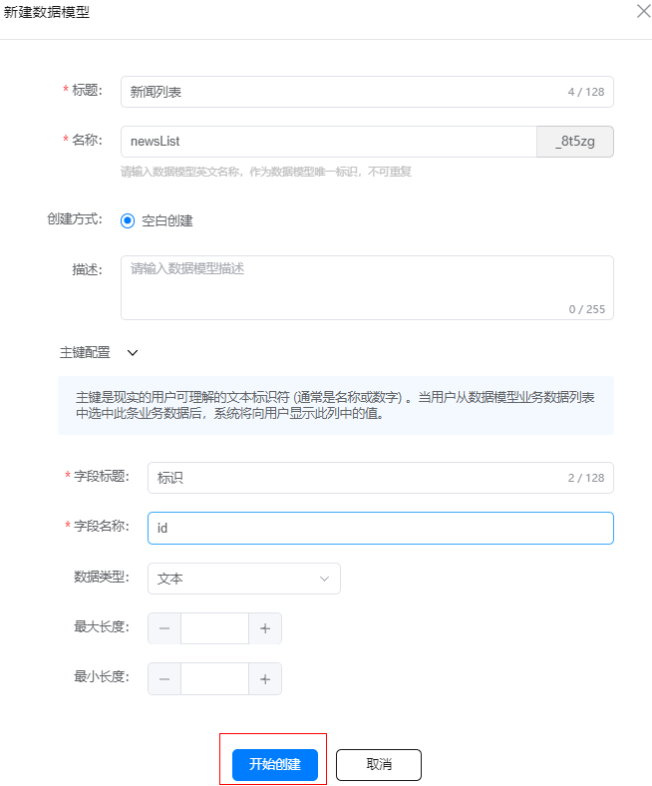
点击开始创建，则成功新建该数据模型：
点击编辑，开始编辑该数据模型，为该数据模型添加需要的其它字段：
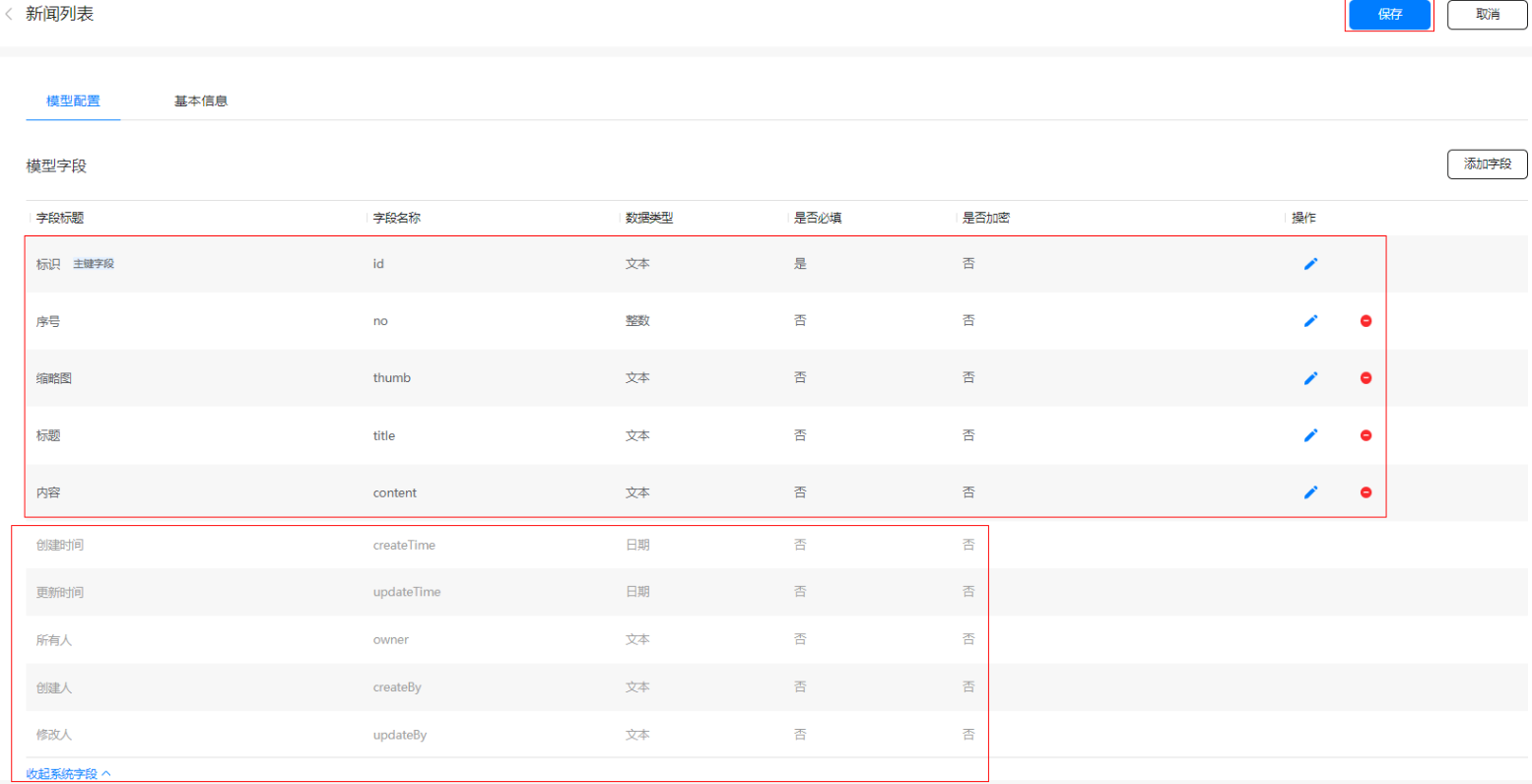
这里为该数据模型新建了序号、缩略图、标题、内容等字段，系统默认生成了创建时间、更新时间、所有人、创建人及修改人几个字段，并且还默认生成了一系列的增删改查的方法：
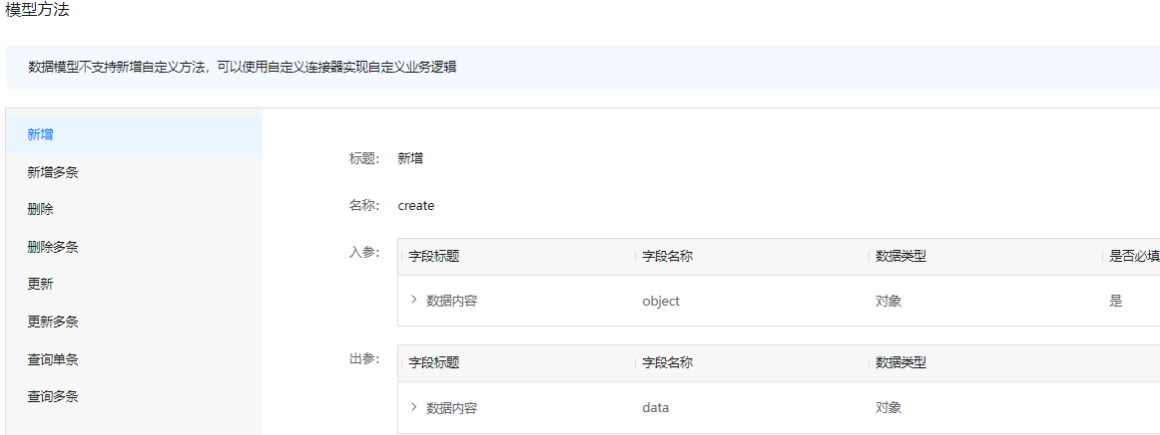
接着点击保存，完成数据模型的更新。
创建完成数据模型之后，需要给该数据模型添加数据，点击数据模型列表中的管理数据：
点击新建开始创建具体数据：
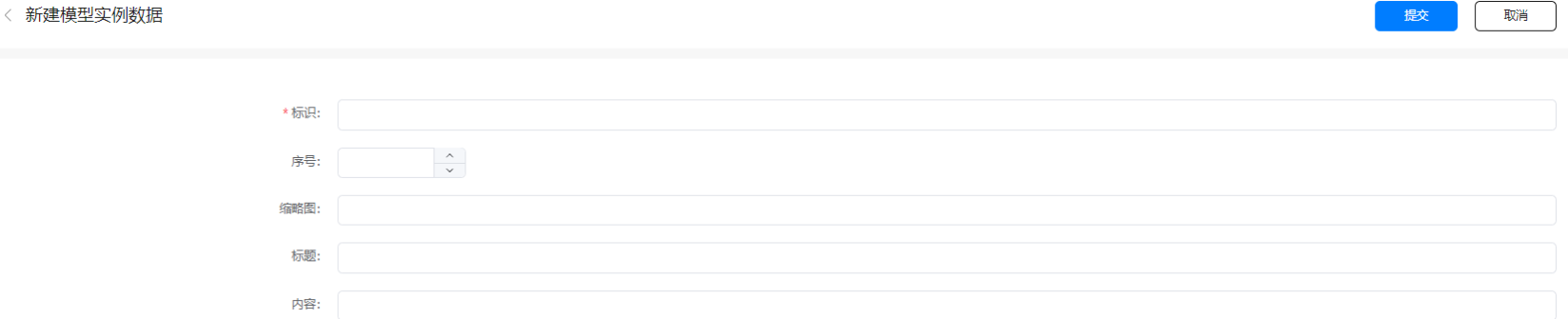
这里简单创建3条数据：
OK，通过以上步骤，云侧的数据模型及数据的添加就已经完成了。
3.3、端云绑定
端侧想要实现绑定云侧创建的数据模型，需要满足两个条件：
①、DevEco Studio需要登录开发者账号：
②、下载agconnect-services.json文件置于应用级根目录下：
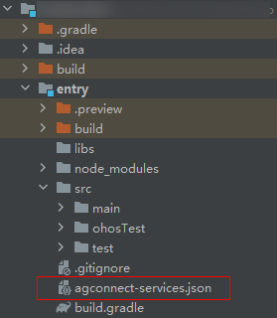
OK，完成了以上步骤之后，就可以开始端云数据绑定的操作啦。
首先在右侧属性样式面板中切换到最下方PageData面板，点击Add Data，选择DataModel：
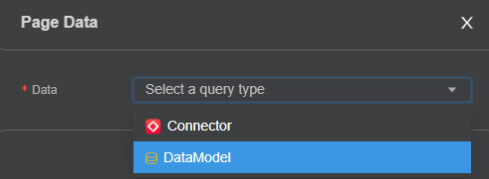
接着选择对应的数据模型，类型这里选择List：
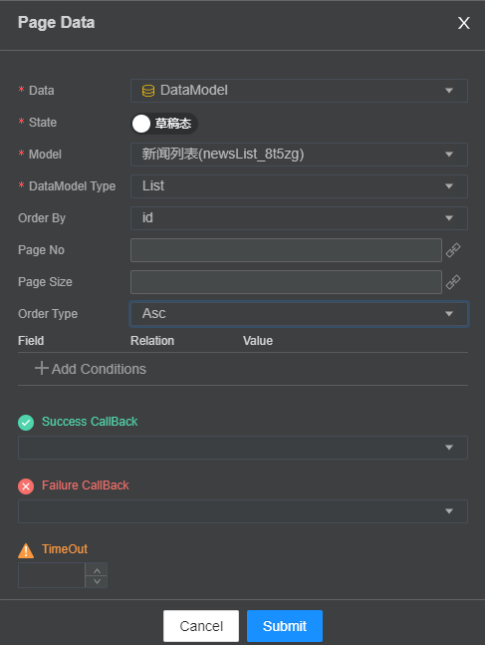
然后选中ListItem组件，为其绑定数据。由于端侧UI需要实现的是一个List列表，所以这里绑定数据通过For来快速实现循环添加数据的能力：
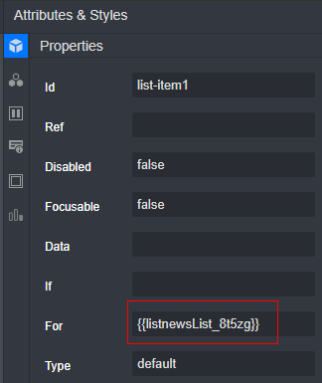
然后依次为Image和右侧的两个Text组件绑定对应的数据字段：
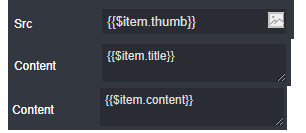
到这里，就完成了端云的数据绑定啦！
3.4、效果展示
下面来看一下最终的实现效果吧：
参考文档：
https://developer.huawei.com/consumer/cn/doc/distribution/app/agc-lowcode-overview-0000001548175386
【HarmonyOS】详解低代码端云一体化开发之数据模型的更多相关文章
- 深度学习之卷积神经网络(CNN)详解与代码实现（一）
卷积神经网络(CNN)详解与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/10430073.html 目 ...
- WebSocket安卓客户端实现详解(三)–服务端主动通知
WebSocket安卓客户端实现详解(三)–服务端主动通知 本篇依旧是接着上一篇继续扩展,还没看过之前博客的小伙伴,这里附上前几篇地址 WebSocket安卓客户端实现详解(一)–连接建立与重连 We ...
- 详解低延时高音质：丢包、抖动与 last mile 优化那些事儿
本篇是「详解低延时高音质系列」的第三篇技术分享.我们这次要将视角放大,从整个音频引擎链路的角度,来讲讲在时变的网络下,针对不同的应用场景,如何权衡音质和互动的实时性. 当我们在讨论实时互动场景下的低延 ...
- Python - 元组(tuple) 详解 及 代码
元组(tuple) 详解 及 代码 本文地址: http://blog.csdn.net/caroline_wendy/article/details/17290967 元组是存放任意元素集合,不能修 ...
- Python - 字典(dict) 详解 及 代码
字典(dict) 详解 及 代码 本文地址: http://blog.csdn.net/caroline_wendy/article/details/17291329 字典(dict)是表示映射的数据 ...
- C#的String.Split 分割字符串用法详解的代码
代码期间,把代码过程经常用的内容做个珍藏,下边代码是关于C#的String.Split 分割字符串用法详解的代码,应该对码农们有些用途. 1) public string[] Split(params ...
- laravel 框架配置404等异常页面的方法详解（代码示例）
本篇文章给大家带来的内容是关于laravel 框架配置404等异常页面的方法详解(代码示例),有一定的参考价值,有需要的朋友可以参考一下,希望对你有所帮助. 在Laravel中所有的异常都由Handl ...
- Android java程序员必备技能，集合与数组中遍历元素，增强for循环的使用详解及代码
Android java程序员必备技能,集合与数组中遍历元素, 增强for循环的使用详解及代码 作者:程序员小冰,CSDN博客:http://blog.csdn.net/qq_21376985 For ...
- 详解 HTTPS 移动端对称加密套件优
近几年,Google.Baidu.Facebook 等互联网巨头大力推行 HTTPS,国内外的大型互联网公司很多也都已启用全站 HTTPS. Google 也推出了针对移动端优化的新型加密套件 Cha ...
- 【转载】 深度学习之卷积神经网络(CNN)详解与代码实现（一）
原文地址: https://www.cnblogs.com/further-further-further/p/10430073.html ------------------------------ ...
随机推荐
- .NetCore中使用分布式事务DTM的二阶段消息
一.概述 二阶段消息是DTM新提出的,可以完美代替现有的事务消息和本地消息表架构.无论从复杂度.性能.便利性还是代码量都是完胜现有的方案. 相比现有的消息架构借助于各种消息中间件比如RocketMQ等 ...
- 《HelloTester》第4期
1.前言 终于到了谈面试的部分了! 我在这也说明一下,有同学说之前简历篇的时候一直在说项目的介绍,而面试官真正关心的是技术啊?我在这做个解释,因为我写的这些文章主要针对的是软件测试的同学,所以其他职位 ...
- [Linux]CentOS7：卸载、安装Java JDK
JDK(Java Development Kit)是Java语言的软件开发工具包,包括Java运行环境.Java开发工具.Java基础类库. JRE(Java Runtime Environment) ...
- python选出一定数量的随机文件到某个文件夹
import os import random import shutil def move_file(target_path, save_path, number): file_list = os. ...
- 一天吃透MySQL面试八股文
什么是MySQL MySQL是一个关系型数据库,它采用表的形式来存储数据.你可以理解成是Excel表格,既然是表的形式存储数据,就有表结构(行和列).行代表每一行数据,列代表该行中的每个值.列上的值是 ...
- react中受控组件与非受控组件--
非受控组件:随用随取 1 render() { 2 return ( 3 <div> 4 <h1>非受控组件</h1> 5 <form action=&quo ...
- [OpenCV-Python] 19 Canny 边缘检测
文章目录 OpenCV-Python:IV OpenCV中的图像处理 19 Canny 边缘检测 19.1 原理 19.1.1 噪声去除 19.1.2 计算图像梯度 19.1.3 非极大值抑制 19. ...
- Driver8833电机驱动模块的使用（STM32为主控）
一.硬件 STM32C8T6.STLINK下载器 Driver8833:TI公司的DRV8833是双桥马达驱动器解决方案,包括有两个H桥驱动器,可驱动两个DC电刷马达,或一个步进马达, 螺线管和其它电 ...
- express服务器框架
Express 为了提高开发效率,我们在开发过程中,都会尽量使用别人已经开发好的第三方模块,而我们想要快速实现服务器端的开发,推荐一个当下比较流行的框架:Express Express 作为开发框架, ...
- 2022-05-16：A -＞ B，表示A认为B是红人， A -＞ B -＞ C，表示A认为B是红人，B认为C是红人，规定“认为”关系有传递性，所以A也认为C是红人， 给定一张有向图，方式是给定M个有
2022-05-16:A -> B,表示A认为B是红人, A -> B -> C,表示A认为B是红人,B认为C是红人,规定"认为"关系有传递性,所以A也认为C是红 ...