我出一道面试题，看看你能拿 3k 还是 30k！

大家好，我是程序员鱼皮。欢迎屏幕前的各位来到今天的模拟面试现场，接下来我会出一道经典的后端面试题，你只需要进行 4 个简单的选择，就能判断出来你的水平是新手（3k）、初级（10k）、中级（15k）还是高级（30k）！

请听题：

题目

MySQL 数据库中的 count(1)、count(*)、count(字段）有什么区别？

请回答

1、它们在功能上有区别么？

A：有区别

B：没区别

答案

有区别。虽然在 MySQL 中，count(*)、count(1) 和 count(字段名) 都是用来 统计行数的聚合函数 。

但 count(*) 和 count(1) 会统计表中所有行的数量，包括 null 值（不会忽略任何一行数据）；而 count(字段名) 只会统计指定字段不为 null 的行数。

恭喜答对的朋友，3k 的 offer 到手啦！

2、count(*) 和 count(1) 谁更快？

A：count(*)

B：count(1)

C：没区别

答案

效率一致，没区别。

关于 count(1) 和 count(*) 谁更快的问题，网上众说纷纭，如果背了不专业的八股文，可能答案就选错咯~

有点经验的程序员，在遇到不确定的问题时，当然要去源头亲自求证，得去看官网怎么说。如图：

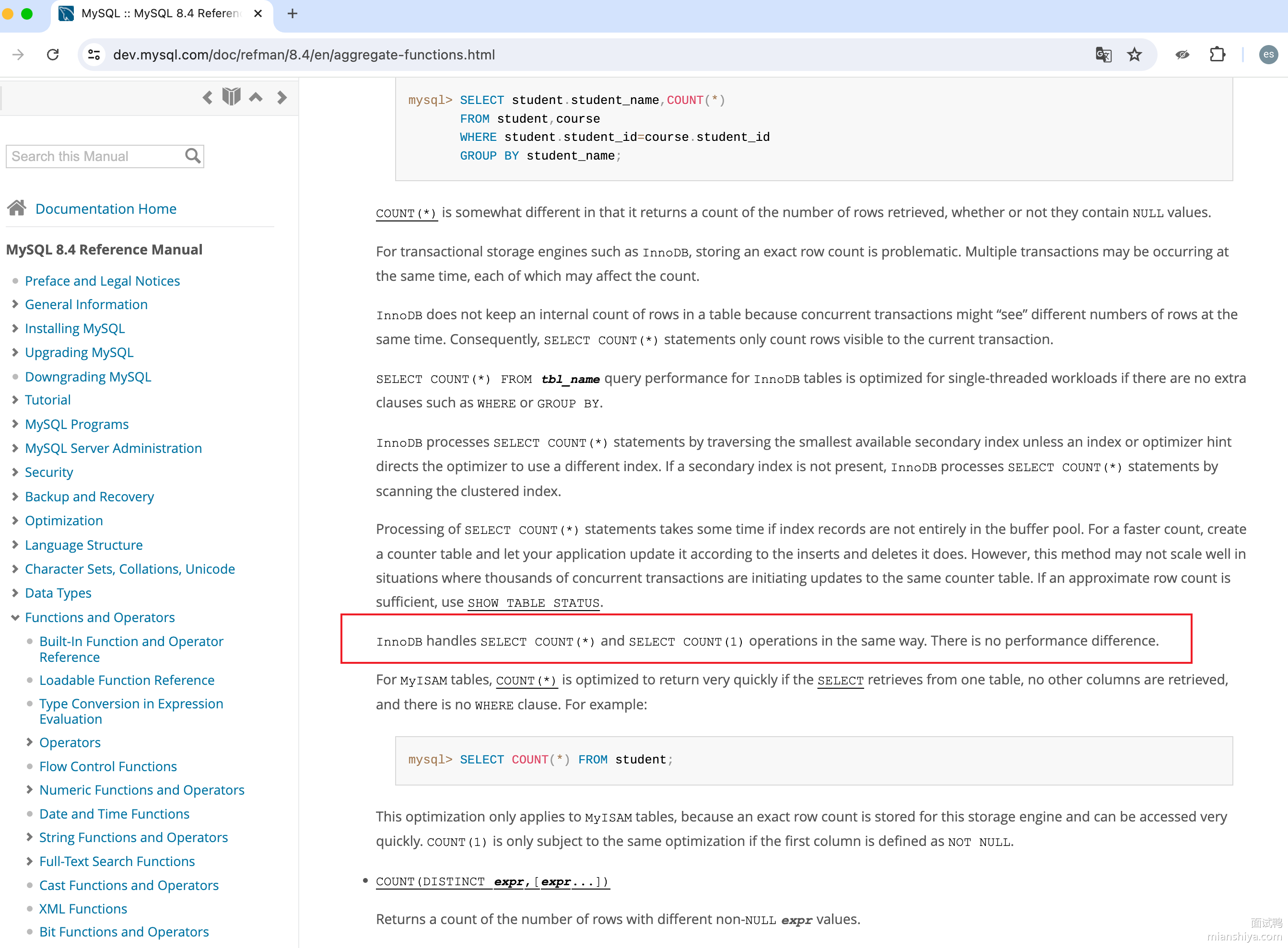
官网表示 There is no performance difference ，即二者没有性能上的区别！

对于 count(字段) 的查询就是全表扫描，正常情况下它还需要判断字段是否是 null 值，因此理论上会比 count(1) 和 count(*) 慢。

但是如果字段不为 null，例如是主键或具有非空约束，那么理论上性能也差不多。而且本质上它们的统计功能不一样，在需要统计 null 的时候，只能用 count(1) 和 count(*)，不需要统计 null 的时候只能用 count(字段)，所以也不用太纠结性能问题。

恭喜答对的朋友，10k 的 offer 到手啦！

3、用 count(*) 统计有千万条记录的表的总数据量，快不快？

A：快

B：慢

C：其他

答案

这是一道简单的场景题，有经验的程序员，本能地会想到 具体情况具体分析 。

MySQL 有 2 个主流的存储引擎 MyISAM 和 InnoDB。

在 MyISAM 引擎中，有一个内部计数器来维护表的记录数，查询时可以直接返回表的行数，而无需扫描整个表，所以 count(*) 非常快。

但是在 InnoDB 引擎中无法维护记录总数，需要扫描整个表，所以表越大、记录越多，count(*) 就越慢。

为什么 InnoDB 引擎不维护记录总数呢？因为它支持行锁，会有很多并发修改表数据的操作，难以维护总数，还会带来额外的性能开销；而 MyISAM 只有表锁，对单个表的修改串行执行，所以能维护总数。所以要针对业务场景选择不同的 MySQL 引擎。

恭喜答对的朋友，15k 的 offer 到手啦！

4、InnoDB 引擎中，count(id) 和 count(二级索引) 哪个成本更低？

A：count(id)

B：count(二级索引)

C：其他

答案

count(二级索引) 通常成本更低。是不是没想到？

这是对上一问的进一步追问，虽然 InnoDB 引擎中 count(*) 统计总数性能不高，但它也针对这个操作进行了一定的优化。

id 通常是主键索引，在 InnoDB 中，主键索引是聚簇索引，它存储了实际的数据行。执行 count 时，InnoDB 需要遍历整个聚簇索引来统计行数。

二级索引是指存储了索引列和主键列的指针，而不包含实际的数据行。因此，二级索引相对来说更小。执行 count 时，InnoDB 只需要遍历这个较小的二级索引，而不是整个聚簇索引，需要读取的数据页更少，所以成本更低。

当然，理论归理论，具体情况具体分析，具体的性能差异取决于索引的大小和表的结构，可以用 explain 语句查看查询计划和成本。

恭喜答对的朋友，30k 的 offer 到手啦！

哦不对，恭喜摸到了 30k 的门槛，继续努力，说不定下一个技术专家就是你~

最后

通过这道题目可以发现，其实面试的时候，很多题目都是可以深挖的，挖的越深，越能体现出候选人的水平。

有同学表示：自己面试题目都答上来了，为啥还是通过不了？

别灰心，可能只是差点儿运气，同场面试有同学比你答的更深、表达更流畅罢了。

不管怎么样，大家在准备面试八股文的时候，有时间的话，多思考一点、再深入一点，自己也能学到很多东西。欢迎多到我们的面试刷题神器 - 面试鸭上看看。

你答对了几问呢？欢迎大家在评论区留言~

编程学习交流：编程导航

简历快速制作：老鱼简历

️ 面试刷题神器：面试鸭