Java 通过先序后序序列生成二叉树

题目

　　二叉树的前序以及后续序列，以空格间隔每个元素，重构二叉树，最后输出二叉树的三种遍历方式的序列以验证。

　　输入：

　　1 2 3 4 5 6 7 8 9 10

　　3 2 5 4 1 7 8 6 10 9

　　输出：

　　1,2,3,4,5,6,7,8,9,10
　　3,2,5,4,1,7,8,6,10,9
　　3,5,4,2,8,7,10,9,6,1

分析

　　以上述输入为例，该树的结构为：

　　　　

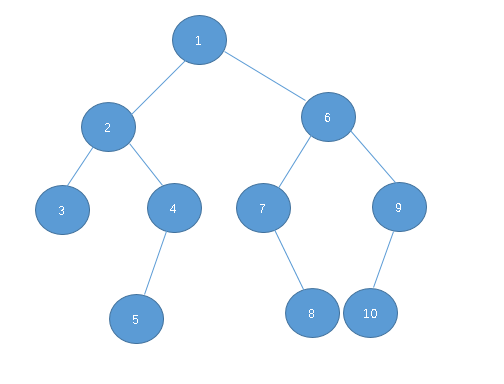
　　在解决这方面问题时，需要把控这几个因素：
　　（1）前序的第一个元素必为根节点；

　　（2）中序中在根节点左边的为左子树，在根节点右边的为右子树。

　　抓住上面两点，就可以无限递归，从而产生一个完整的二叉树。

算法演算

　　　前序：1 2 3 4 5 6 7 8 9 10

　　　中序：3 2 5 4 1 7 8 6 10 9

　　　　

　　　　<默认优先处理左子树>

　　　（1）第一次：

　　　　　　产生节点 1。

　　　　　　生成左子树

　　　　　　　　　　先序：2 3 4 5

　　　　　　　　　　中序：3 2 5 4

　　　　　　生成右子树

　　　　　　　　　　前序：6 7 8 9 10

　　　　　　　　　　中序：7 8 6 10 9

　　　　（2）第二次

　　　　　　　产生节点 2（由左子树得来，故为第一次结点的左子树）。

　　　　　　　生成左子树

　　　　　　　　　　前序：3

　　　　　　　　　　中序：3

　　　　　　　生成右子树

　　　　　　　　　　先序：4 5

　　　　　　　　　　中序：5 4

　　　　（3）第三次

　　　　　　  产生节点 3（同上，产生左子树）

　　　　　　  <此处限定：当先序长度小于等于1时，直接Return>

　　　　(4)第四次（因为Return，所以处理第二次产生的右子树）

　　　　　　 产生结点 4

　　　　　　 生成左子树

　　　　  　　　　   先序：null

　　　　　　　　　  中序：null

　　　　　　 生成右子树

　　　　　　　　　　先序：5

　　　　　　　　　　后续：5

　　　　　 <此处限定：当新生成的左（右）序列为空时，则只进行右（左）序列的处理,并将为空的节点初始化为null>

　　

　　　　……

　　　　以此类推，即可轻松生成一棵二叉树。

实现代码

package DataStructe;

import java.util.ArrayList;
import java.util.Scanner;

public class TreeReBuild {
    /*先序（DLR）、中序（LDR）遍历对应的三个数组*/
    static ArrayList<Integer> DLR=new ArrayList<Integer>();
    static ArrayList<Integer> LDR=new ArrayList<Integer>();
    static node root=new node();

    /*二叉树的结点结构*/
    static class node{
        node rchild;
        node lchild;
        int data;
        node(int ndata)
        {
            data=ndata;
            rchild=null;
            lchild=null;
        }
        public node() {
            rchild=null;
            lchild=null;
        }
    }

    /*核心算法*/
    static void reBuildTreeprocess(node x,ArrayList<Integer> qx,ArrayList<Integer> zx)
    {
        x.data=qx.get(0);//前序第一个元素必为根节点
        if(qx.size()<=1)
        {
            return;
        }
        x.lchild=new node();
        x.rchild=new node();
        //两个序列的拆分索引
        int rootindex = 0;
        int qxindex=0;
        /*拆分序列*/
        ArrayList<Integer>newqxleft    = new ArrayList<Integer>();
        ArrayList<Integer>newqxright= new ArrayList<Integer>();
        ArrayList<Integer>newzxleft = new ArrayList<Integer>();
        ArrayList<Integer>newzxright = new ArrayList<Integer>();
        //拆分中序
        for(int j=0;j<zx.size();j++)
        {
            if(zx.get(j)==x.data)
            {
                zx.remove(j);
                j--;
                rootindex=j;
                break;
            }
        }

        //生成新的中序（左）
        for(int j=0;j<=rootindex;j++){

            newzxleft.add(zx.get(j));
        }
        //生成新的中序（右）
        for(int j=rootindex+1;j<zx.size();j++)
        {
            newzxright.add(zx.get(j));
        }

        //拆分前序，确定分离的元素索引
        if(newzxright.isEmpty())
        {
            //中序右为空，前序全为左子树
            for(int i=1;i<qx.size();i++)
            {
                newqxleft.add(qx.get(i));
            }
            x.rchild=null;
            reBuildTreeprocess(x.lchild, newqxleft, newzxleft);
        }
        else{
            if(newzxleft.isEmpty())
            {
                //中序左为空，前序全为右子树
                for(int i=1;i<qx.size();i++)
                {
                    newqxright.add(qx.get(i));
                }
                x.lchild=null;
                reBuildTreeprocess(x.rchild, newqxright, newzxright);
            }
            else {
                //均不为空，分别生成
                outer:        for(int r=0;r<qx.size();r++)
                {

                    for(int i=0;i<newzxright.size();i++)
                    {

                        if(qx.get(r)==newzxright.get(i))
                        {

                            qxindex=r;
                            break outer;
                        }
                    }
                }

            for(int t=1;t<qxindex;t++)
            {
                newqxleft.add(qx.get(t));
            }
            for(int y=qxindex;y<qx.size();y++)
            {
                newqxright.add(qx.get(y));
            }
            reBuildTreeprocess(x.lchild, newqxleft, newzxleft);
            reBuildTreeprocess(x.rchild, newqxright, newzxright);
            }
        }
    }
    /*先序遍历，用于测试结果*/
    static void XSearch(node x)
    {
        if (x==null) {
            return;
        }
        System.out.print(x.data+",");
      if (x.lchild!=null) {
          XSearch(x.lchild);
        }

      if(x.rchild!=null){
          XSearch(x.rchild);
          }
    }

    /*中续遍历,用于测试结果*/
    static void ZSearch(node x)
    {
        if (x==null) {
            return;
        }
      if (x.lchild!=null) {
          ZSearch(x.lchild);
        }
      System.out.print(x.data+",");
      if(x.rchild!=null){
          ZSearch(x.rchild);
          }

    }

    /*后续遍历，用于测试结果*/
    static void HSearch(node x)
    {
        if (x==null) {
            return;
        }
      if (x.lchild!=null) {
          HSearch(x.lchild);
        }
      if(x.rchild!=null){
          HSearch(x.rchild);
          }
      System.out.print(x.data+",");
    }

    public static void main(String[] args) {
        Scanner getin=new Scanner(System.in);

        /*读入先序序列*/
        String readydata=getin.nextLine();
        String []DLRdata=readydata.split(" ");
        for(int i=0;i<DLRdata.length;i++)
        {
            int qxdata=Integer.parseInt(DLRdata[i]);
            DLR.add(qxdata);
        }

        /*读入中序序列*/
        readydata=getin.nextLine();
        String[]LDRdata=readydata.split(" ");
        for(int i=0;i<LDRdata.length;i++)
        {
            int zxdata=Integer.parseInt(LDRdata[i]);
            LDR.add(zxdata);
        }
        reBuildTreeprocess(root, DLR, LDR);

        XSearch(root);
        System.out.println();
        ZSearch(root);
        System.out.println();
        HSearch(root);
        System.out.println();

    }

}