两道二分coming~

第一道：poj 1905Expanding Rods

题意：两道墙（距离L）之间架一根棒子，棒子受热会变长，弯曲，长度变化满足公式（ s=(1+n*C)*L），求的是弯曲的高度h。

首先来看这个图：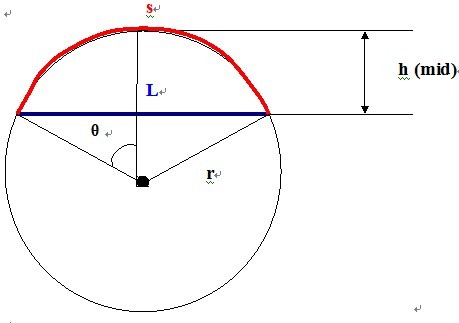

如图，蓝色为杆弯曲前，长度为L

红色为杆弯曲后，长度为s

h是所求。

又从图中得到三条关系式;

（1）       角度→弧度公式  θr = 1/2*s

（2）       三角函数公式  sinθ= 1/2*L/r

（3）       勾股定理  r^2 – ( r – h)^2 = (1/2*L)^2

把四条关系式化简可以得到

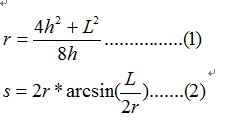
逆向思维解二元方程组：

要求（1）式的h，唯有先求r

但是由于（2）式是三角函数式，直接求r比较困难

因此要用顺向思维解方程组：

在h的值的范围内枚举h的值，计算出对应的r，判断这个r得到的(2)式的右边  与 左边的值S的大小关系  （ S= (1+n*C)*L ）

很显然的二分查找了。。。。。

看代码：

 #include<stdio.h>
 #include<string>
 #include<math.h>
 #include<string.h>
 #include<algorithm>
 #define esp 1e-5
 using namespace std;
 int main()
 {
     double l,n,c,s,h,r;
     while(scanf("%lf%lf%lf",&l,&n,&c)!=EOF)
     {
         if(l==-&&n==-&&c==-)
             break;
         s=(+n*c)*l;
         double low=0.0,high=l*0.5,mid;
         while(high-low>esp)
         {
             mid=(low+high)/;
             r=(*mid*mid+l*l)/(*mid);
             if(*r*asin(l/(*r))<s)
                 low=mid;
             else
                 high=mid;
         }
         printf("%.3lf\n",mid);
     }
     return ;
 }

第二题：poj 3122 Pie

题意：f+1个人分n个派。

要求：每个人的派的体积一样大且尽量最大，每个人的派必须来自同一个派。

二分题，千万要注意，输入的是朋友的数量f，分pie是分给所有人，包括自己在内共f+1人

下界low=0，即每人都分不到pie

上界high=maxsize，每人都得到整个pie，而且那个pie为所有pie中最大的

对当前上下界折中为mid，计算"如果按照mid的尺寸分pie，能分给多少人"

求某个pie（尺寸为size）按照mid的尺寸，能够分给的人数，就直接size / mid，舍弃小数就可以

看代码：

#include<stdio.h>
#include<string>
#include<math.h>
#include<string.h>
#include<algorithm>
#define pi 3.14159265359
#define esp 1e-6
using namespace std;
int main()
{
    int t;
    int n,f,maxs;
    double v;
    double r[];
    double s[];
    scanf("%d",&t);
    while(t--)
    {
        maxs=0.0;
        int ans=;
        scanf("%d%d",&n,&f);
        f++;
        for(int i=;i<n;i++)
        {
            scanf("%lf",&r[i]);
            s[i]=r[i]*r[i];
            if(maxs<s[i])
                maxs=s[i];
        }
        double low=0.0,high=maxs,mid;
        while(high-low>esp)
        {
            mid=(low+high)/;
            ans=;
            for(int i=;i<n;i++)
            {
                ans+=(int)(s[i]/mid);
            }
            if(ans<f)
                high=mid;
            else
                low=mid;
        }
        printf("%.4lf\n",mid*pi);
    }
    return ;
}