利用charles映射解决夜神模拟器安装xposed-v89-sdk25-x86.zip

最近在玩xposed框架，前前后后搞了两天，浪费一个周末，总算把踩过的坑都踩了一遍。。

比如大家肯定遇到的的一个问题：夜神模拟器打开xposed安装器之后，为什么下载不了xposed-v89-sdk25-x86.zip这些框架包呢？

那是因为访问地址已经由http变成https啦，原来的地址相当于失效了。

通过charles抓包可以得知，在xposed安装器界面下拉的时候（图一），都会有一条这样的请求（图二）

图一

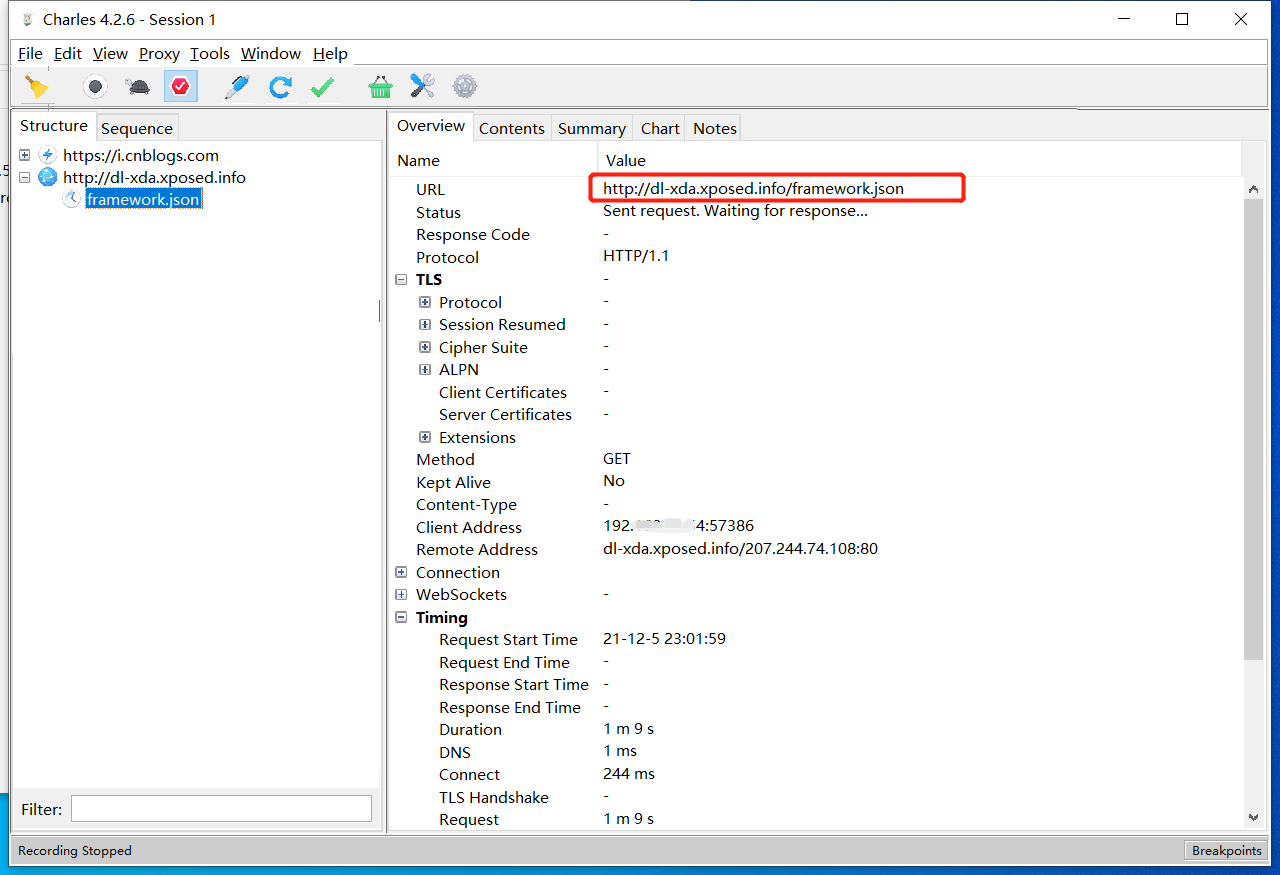
图二

这条请求：http://dl-xda.xposed.info/framework.json，就相当于通过它去访问框架包的下载地址

但xposed地址已经变成https了，所以就算访问得了，也是下载失败的，这就像一道墙挡住了那样，懂了吧。。

下拉刷新完毕，会出现以下界面，我们点一下，尝试着下载89版本，然后看看charles的请求。

好，我们基本知道有两个请求地址的，分别是：

请求框架包路径的地址：http://dl-xda.xposed.info/framework.json

下载框架包的地址：http://dl-xda.xposed.info/framework/sdk22/x86/xposed-v89-sdk22-x86.zip

下一步我们要通过charles映射，把http指向https

打开charles-Tools-Map Remote Settings，设置远程映射

由http://dl-xda.xposed.info/framework.json，

指向https://dl-xda.xposed.info/framework.json

保存，

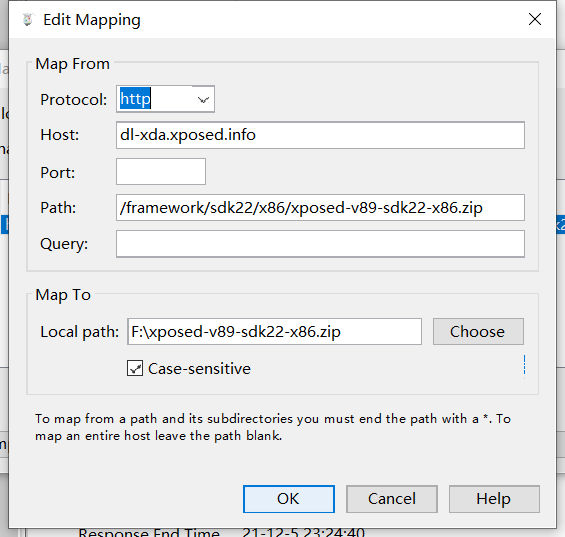
然后设置本地映射，打开charles-Tools-Map Local Settings

其中，F:\xposed-v89-sdk22-x86.zip是你本地存放框架包的路径。

那么问题又来了，我的这个xposed-v89-sdk22-x86.zip是哪里得来的呢？

其实是通过https://dl-xda.xposed.info/framework/下载得到的，如下图：

自己下载框架包之后，放在C盘或D盘根目录，我是放F盘根目录的。

设置本地映射，意思是原本通过http://dl-xda.xposed.info/framework/xposed-v89-sdk22-x86.zip去下载包，那我现在直接让它去F:/xposed-v89-sdk22-x86.zip下载。

远程映射、本地映射都设置好了，

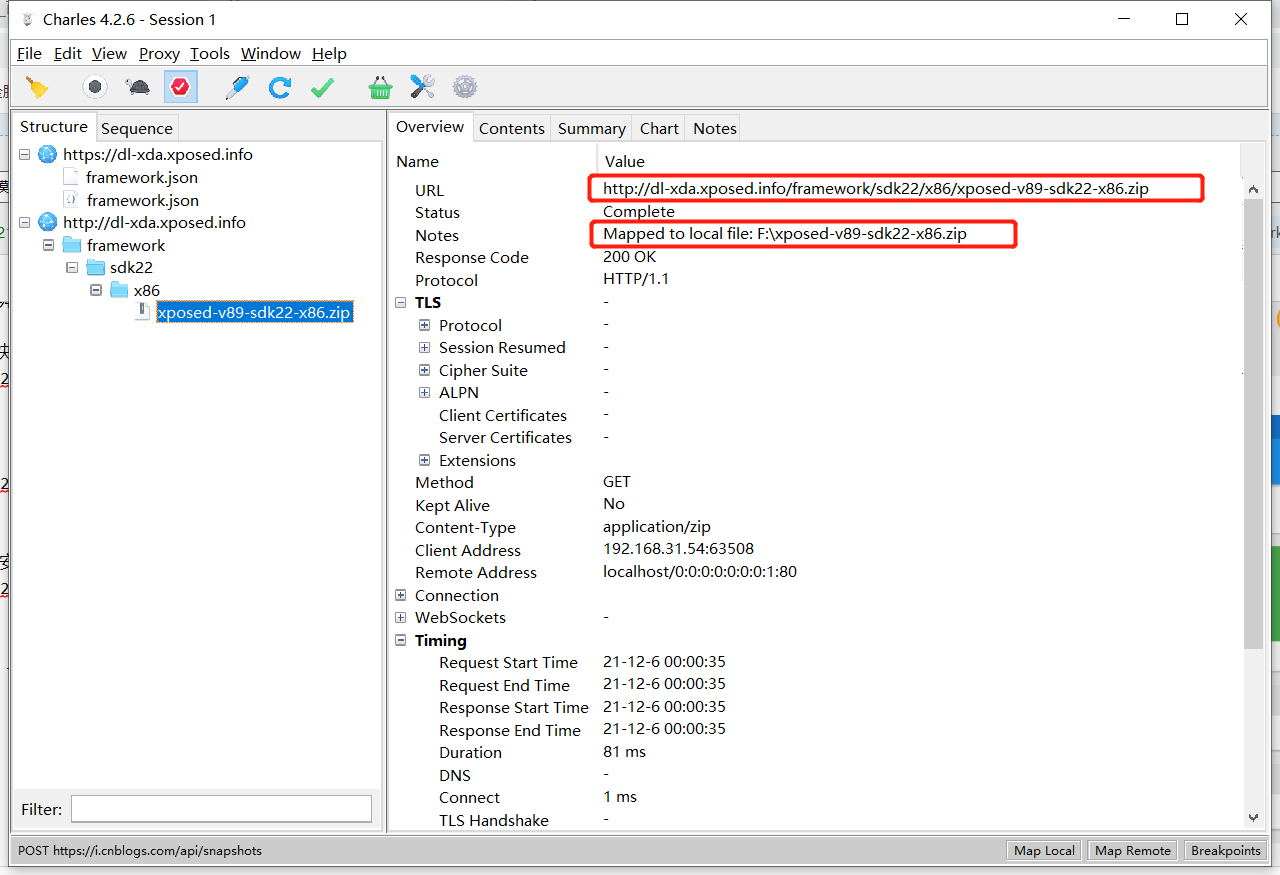
我们打开夜神模拟器，打开xposed安装器，下拉，点击Version 89，install，注意了，因为设置了本地映射，这时候的xposed安装器是直接访问我的F盘根目录，去下载本地的框架包，所以你会看到它的下载是很快的，一瞬间就完成，这也说明通过映射可以成功让xposed安装器装上了框架包！

你看，本地下载特别快，直接进入安装界面了！（选择永久授权）

安装好，重启模拟器

重启，再打开xposed安装器，可以看到框架已经激活了！

• • • -分割线 - - -

大家看到这个请求了么，原本是去http://dl-xda.xposed.info/framework/xposed-v89-sdk22-x86.zip下载框架包的，现在指向F盘下载。

这个呢其实就是运用了抓包工具的一个小技巧，映射，完美地解决了xposed无法下载框架包的问题，一开始我还以为访问外网的缘故，导致下载速度很慢，后来才明白，既然是外网，那就别想了，我昨天搞了一天，有些人说要挂梯子，哎，下载一个这么小的东西，还用得着挂梯子。。现在有了映射，直接修改地址不就得了。