matlab与python scipy.signal中 freqs freqz 中w,什么时候是角频率，什么时候是真实的工程中使用的采样频率Hz,如何转化

matlab与python scipy.signal中的freqs,freqz频率分析函数，输出的w，有时候是角频率，有时候是真实频率，容易搞混，这里对比一下。

0. 精要总结：

　　1) freqs:

　　　　matlab, 角频率，rad.s

　　　　python, 角频率 rad/s ,只能是角频率。

　　2) freqz

　　　　matlab, 形式为 [h,w] = freqz(b,a,n) 角频率

　　　　　　　　形式为 [h,f] = freqz(___,n,fs) 时，频率输出形式f为Hz形式，fs为采样频率

　　　　python scipy 中 w,h =freqz(b,a,worN,fs) ， w的单位与输入fs相同，fs为归一化角频率时，w也为角频率，fs为采样频率，单位Hz时，w也为Hz。

　　3) 角频率范围的区别：

　　　　freqs中的角频率是现实中的量，可以很大，比如1000Hz，对应的角频率为1000*2*pi ; freqz中的角频率是数字化的，一般使用时是归一化的，范围在 0，2*pi之间。

　　4) 角频率与Hz频率转化：

　　　　freqs的w结果要想用Hz,显示，可以先 w/2/pi 转化为 Hz 频率； freqz中的角频率如果要转化为具体的频率，因为他是归一化的，用 0~ pi 的范围代表 0- fs/2 的频率范围，可以用 f=（ w/pi）*（fs/2）转化为Hz频率

1. freqs

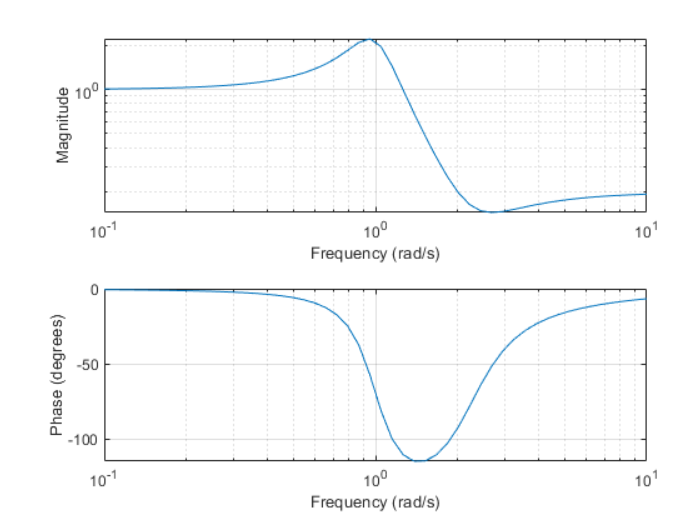
1.1 matlab中

freqs 是角频率w的单位 rad/s，想要变成Hz, 显示时使用 f = w/2/pi

模拟的freqs不存在归一化。

a = [1 0.4 1];
b = [0.2 0.3 1];
w = logspace(-1,1);
 
h = freqs(b,a,w);
mag = abs(h);
phase = angle(h);
phasedeg = phase*180/pi;
 
subplot(2,1,1)
loglog(w,mag)
grid on
xlabel('Frequency (rad/s)')
ylabel('Magnitude')
 
subplot(2,1,2)
semilogx(w,phasedeg)
grid on
xlabel('Frequency (rad/s)')
ylabel('Phase (degrees)')

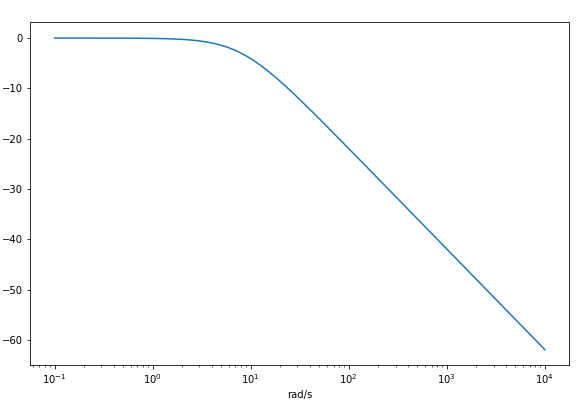
1.2 python scipy.signal 中

freqs 输出的w也是rad/s，也只能是rad/s 角频率。不过这个不是归一化的。模拟的freqs不存在归一化。

w : ndarray

　　The angular frequencies at which `h` was computed.

b = [1]
a = [0.125 ,1]
 
#         b(0) *s^0
#  s = ----------------
#     a(0)*s^1 +a(1)*s^0
 
from scipy.signal import bilinear,freqs,freqz
import  matplotlib.pyplot   as plt
import numpy as np
 
# %% python scipy.signal 中 freqs
wf=np.logspace(-1, 4, 1000)
w,h = freqs(b,a,wf)
 
plt.semilogx(w,20*np.log10(np.abs(h)))
plt.xlabel('rad/s')

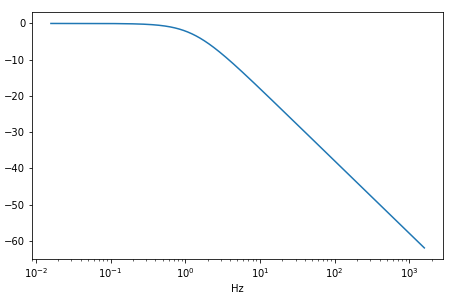
如何转化为Hz显示，就是x坐标轴除以 2*pi

b = [1]
a = [0.125 ,1]
 
#         b(0) *s^0
#  s = ----------------
#     a(0)*s^1 +a(1)*s^0
 
from scipy.signal import bilinear,freqs,freqz
import  matplotlib.pyplot   as plt
import numpy as np
 
# %% python scipy.signal 中 freqs
wf=np.logspace(-1, 4, 1000)
w,h = freqs(b,a,wf)
 
# plt.semilogx(w,20*np.log10(np.abs(h)))
# plt.xlabel('rad/s')
 
plt.semilogx(w/2/np.pi,20*np.log10(np.abs(h)))
plt.xlabel('Hz')

2. freqz

2.1 matlab中

1) 函数形式为

[h,w] = freqz(b,a,n)

时，w输出为角频率，且归一化，即最大的角频率为 pi (对应fs/2,归一化处理) 。（n为输出的点的个数）和freqs中

2) 函数形式为

[h,f] = freqz(___,n,fs)

时，频率输出形式f为Hz形式，fs为采样频率。

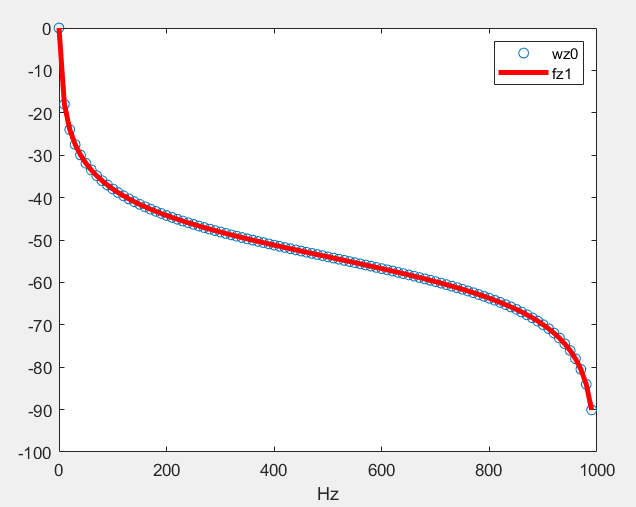
b=1;
a=[0.125 1];
fs=2000;
[bz,az] = bilinear(b,a,fs);
[hz0,wz0] = freqz(bz,az,100); % 100是 n，输出点的个数
fz0= wz0/pi*fs/2;  % 将 归一化的rad/s 转化为 实际的采样频率
plot(fz0,20*log10(abs(hz0)),'o');
xlabel('Hz')
hold on
[hz1,fz1] = freqz(bz,az,100,fs);
plot(fz1,20*log10(abs(hz1)),'r-','linewidth',3);
legend('wz0' , 'fz1')
hold off

　　结果：

2.2 Python scipy.signal 中

freqz(b,a=1, worN=512, whole=False, plot=None, fs=2*pi, include_nyquist = False,)

Returns

-------

w : ndarray

The frequencies at which `h` was computed, in the same units as `fs`.

By default, `w` is normalized to the range [0, pi) (radians/sample).

w的单位和输入fs的单位相同，如果fs是用的 rad/s则返回w也是rad/s，若输入fs的单位是 Hz,那么输出的w单位也是Hz。

代码部分

from scipy.signal import bilinear,freqs,freqz
import  matplotlib.pyplot   as plt
import numpy as np
 
#         b(0) *s^0
#  s = ----------------
#     a(0)*s^1 +a(1)*s^0
 
b = [1]
a = [0.125 ,1]
 
# %% python scipy.signal 5000中 freqs
wf=np.logspace(-1,4,1000 )
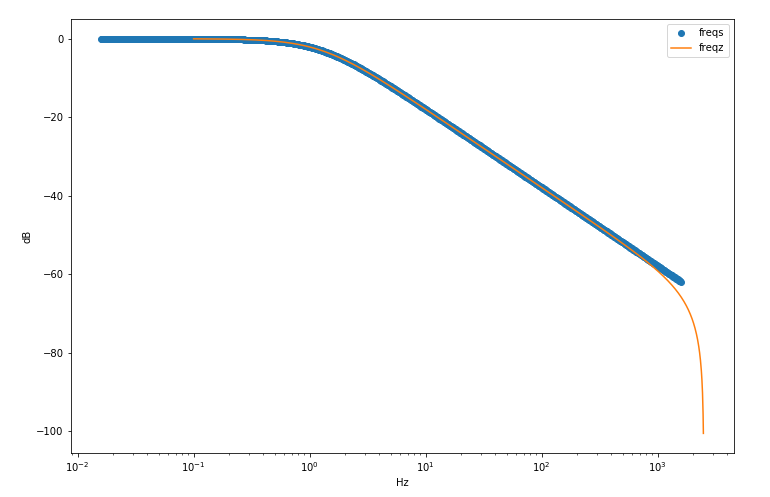
w,h = freqs(b,a,wf)
 
plt.semilogx(w/2/np.pi,20*np.log10(np.abs(h)),'o',label='freqs')
plt.xlabel('Hz')
plt.ylabel('dB')
 
fs=5000
bz,az = bilinear(b,a,fs)
 
worN=np.logspace(-1,4,2000)
idx_end = np.nonzero(worN<=fs/2)[0][-1]
z = freqz(bz,az,worN=worN[0:idx_end],fs=fs)
 
plt.semilogx(z[0],20*np.log10(z[1]),'-',label='freqz')
plt.legend()