JQuery 和 CSS 等选择器:
JQuery 选择器:
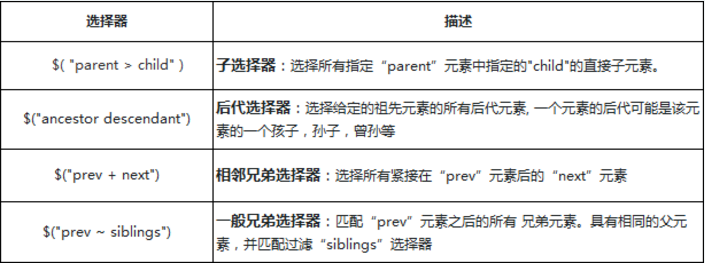
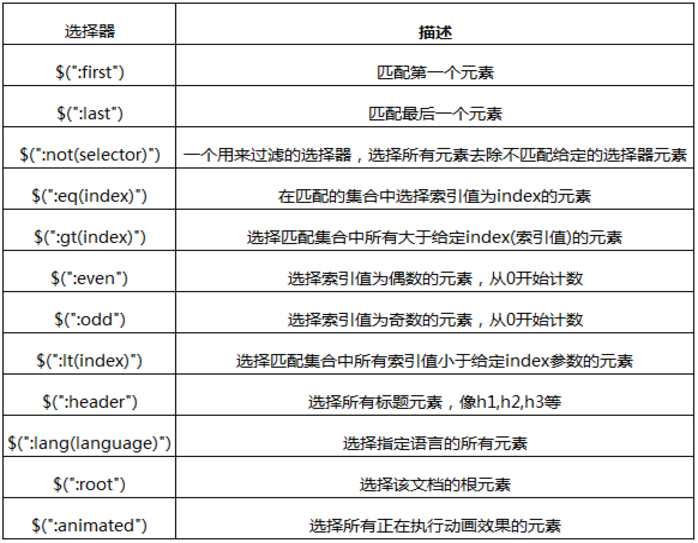

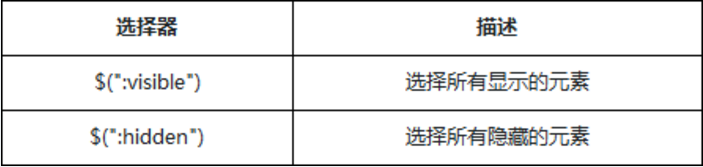
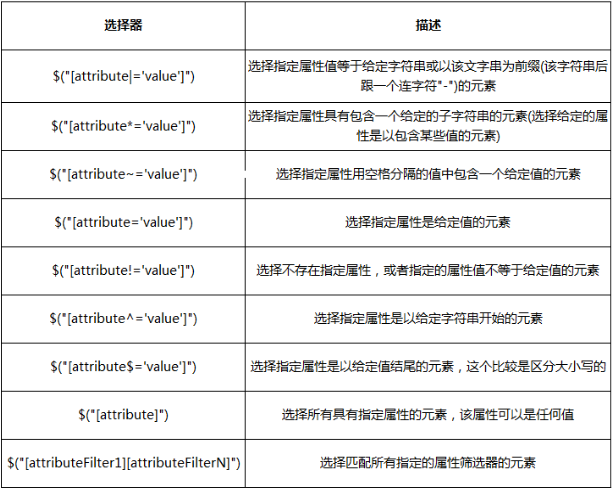
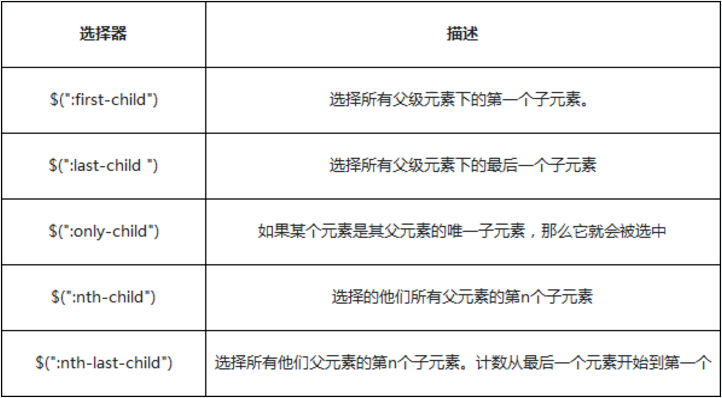
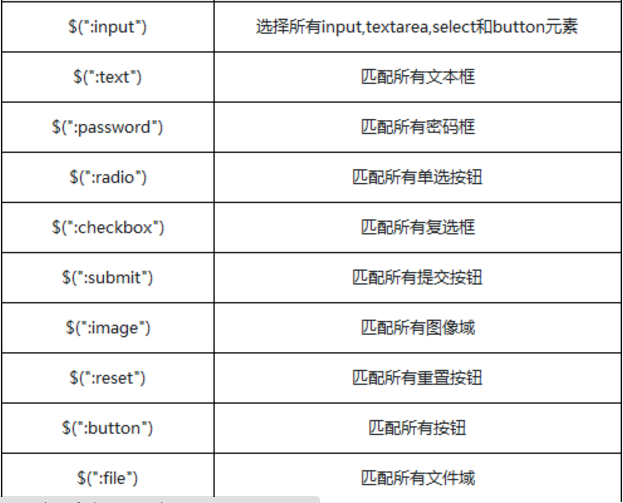
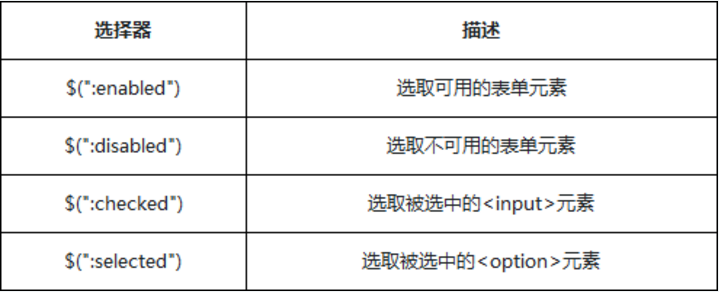
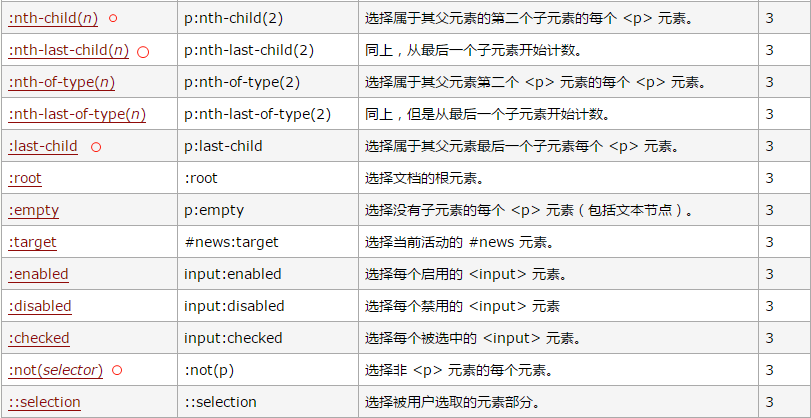
CSS 选择器:
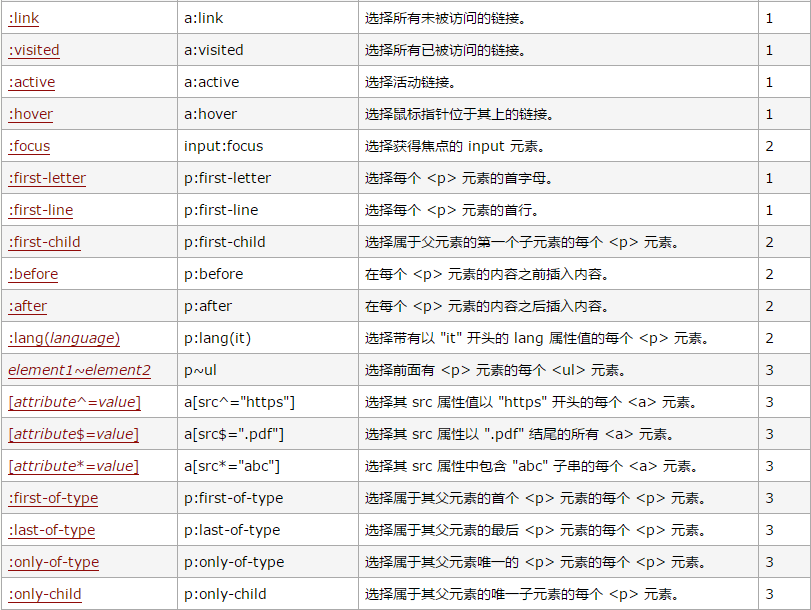
JQuery 和 CSS 等选择器:的更多相关文章
- 前端笔记之jQuery(上)加载函数的区别&对象&操作HTML/CSS&动画&选择器
一.jQuery简介 1.0 JavaScript编程比较恶心的地方 恶心1:选择元素麻烦,全线兼容的方法只有getElementById()和getElementsByTagName()两个.其他的 ...
- CSS的选择器
<div id="demo"> <div class="inner"> <p><a href="#" ...
- jQuery入门(1)jQuery中万能的选择器
jQuery入门(1)jQuery中万能的选择器 jQuery入门(2)使用jQuery操作元素的属性与样式 jQuery入门(3)事件与事件对象 jQuery入门(4)jQuery中的Ajax()应 ...
- jquery笔记之属性选择器 查找以某种条件开头的页面元素
jquery笔记之属性选择器 查找以某种条件开头的页面元素 转载:http://www.blogbus.com/amyqiong-logs/78340326.html $("div[id]& ...
- 从零开始学习jQuery (二) 万能的选择器
本系列文章导航 从零开始学习jQuery (二) 万能的选择器 一.摘要 本章讲解jQuery最重要的选择器部分的知识. 有了jQuery的选择器我们几乎可以获取页面上任意的一个或一组对象, 可以明显 ...
- jquery和css自定义video播放控件
下面介绍一下通过jquery和css自定义video播放控件. Html5 Video是现在html5最流行的功能之一,得到了大多数最新版本的浏览器支持.包括IE9,也是如此.不同的浏览器提供了不同的 ...
- IE7浏览器下CSS属性选择器二三事
一.为何专门说起IE7 以前,或者说数年前,我们从事桌面端网页开发的时候,基本上都还要兼顾IE6浏览器, 即使有些特性,IE7支持,我们也会忽略之.于是,我们会不自然地把IE6和IE7浏览器归为一路货 ...
- JQuery - 改变css样式
jQuery提供css()的方法来实现嵌入式改变元素样式,css()方法在使用上具有多样性.其中一种接受两个输入参数:样式属性和样式值,它们之间用逗号分开.比如我们要改变链接颜色,我们可以使用下面的代 ...
- jQuery(2)——选择器
选择器 利用jQuery选择器,可以非常便捷和快速地找出特定的DOM元素,然后为它们添加相应的行为.jQuery的行为规则都必须在获取到元素后才能生效. [jQuery选择器的优势] (1)简洁的写法 ...
随机推荐
- 从 ThreadLocal 到 AsyncLocal
前些天跟大佬们在群里讨论如何在不使用构造函数,不增加方法参数的情况下把一个上下文注入到方法内部使用,得出的结论是 AsyncLocal .感叹自己才疏学浅,居然才知道有 AsyncLocal 这种神器 ...
- 第三章 sql 的约束
1.0 约束分类 约束类型: 主键 默认值 唯一 外键 非空 关键字: PRIMARY KEY DEFAULT UNIQUE FOREIGN NOT NULL 2.0 建立含约束的表 3.0 主 ...
- [atAGC006D]Median Pyramid Hard
二分答案,考虑答案是否会大于等于这个mid,显然所有数值分为两类:大于等于mid和小于mid将n个数转化为01串,如果0和1不相邻,那么答案就是第一个数/最后一个数(一定会相同),考虑有连续两个0/1 ...
- javascript-初级-day01-属性操作、图片切换、短信发送模拟
大多数js就是操作一些css和html的技巧,如果你会html和css学习js更加轻松哦! js中如何获取元素: 通过id名称来获取元素; document get element by id 'li ...
- CF708E Student's Camp
麻麻我会做*3100的计数了,我出息了 考虑朴素DP我们怎么做呢. 设\(f_{i,l,r}\)为第\(i\)层选择\(l,r\)的依旧不倒的概率. \(q(l,r)\)表示经历了\(k\)天后,存活 ...
- 洛谷 P4621 - [COCI2012-2013#6] BAKTERIJE(exCRT)
洛谷题面传送门 发篇正常点的题解. 首先对于这样的题暴力枚举肯定是不行的,因为最小时间显然可能达到 \((4nm)^5\approx 10^{20}\),就算数据很难卡到这个上界,构造出一些使你暴力超 ...
- 基因组共线性分析工具MCScanX
软件简介 MCScanX工具集对MCScan算法进行了调整,用于检测共线性和同线性区域,还增加了可视化和下游分析..MCscanX有三个核心工具,以及12个下游分析工具. 软件安装 进入官网http: ...
- KVM原理
虚拟化是云计算的基础.简单的说,虚拟化使得在一台物理的服务器上可以跑多台虚拟机,虚拟机共享物理机的 CPU.内存.IO 硬件资源,但逻辑上虚拟机之间是相互隔离的.物理机我们一般称为宿主机(Host), ...
- requests+bs4爬取豌豆荚排行榜及下载排行榜app
爬取排行榜应用信息 爬取豌豆荚排行榜app信息 - app_detail_url - 应用详情页url - app_image_url - 应用图片url - app_name - 应用名称 - ap ...
- react native 导航器 Navigator 简单的例子
最近学习react native 是在为全栈工程师而努力,看网上把react native说的各种好,忍不住学习了一把.总体感觉还可以,特别是可以开发android和ios这点非常厉害,刚开始入门需要 ...
