Codeforces 185D（发现性质、欧拉定理）

学到的东西

• 不知道gcd时不妨先假设为d，然后为了满足全部式子说不定可以得到d的取值范围。
• 幂上带幂考虑欧拉定理的使用。
• 有几个特殊情况会破坏公式的完美不要紧，看看特殊情况是否能简便地判定。
• 连乘公式，证明方法是右边分母乘到左边就都消了：
  
  

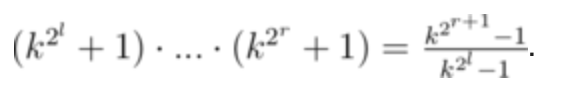
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
int T, k, p;
ll l, r;

ll ksm(int a, ll b, int mod) {
	ll res = 1;
	for (; b; b >>= 1) {
		if (b & 1)	res = res * a % mod;
		a = (ll)a * a % mod;
	}
	return res;
}

ll calc(int k, ll l, ll r, int p) {
	if (k % p == 0)	return 1;//欧拉定理的前提是k、p互质
	ll t = ksm(2, l, p - 1);
	ll q = (ksm(k, t, p) - 1 + p) % p;
	if (!q)	return ksm(2, r - l + 1, p);//分母为0

	ll y = ksm(2, r + 1, p - 1);
	ll res = (ksm(k, y, p) - 1 + p) % p * ksm(q, p - 2, p) % p;
	return res;
}

int main() {
	ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);

	for (cin >> T; T--;) {
		cin >> k >> l >> r >> p;
		if (p == 2) {
			cout << (k % 2 ? 0 : 1) << '\n';
		} else {
			ll MUL = calc(k, l, r, p);
			if (k % 2) {
				MUL = MUL * ksm(ksm(2, r - l, p), p - 2, p) % p;
			}
			cout << MUL << '\n';
		}
	}
}