Symmetric Tree（DFS，二叉树的构建以及测试代码）

基础有待加强啊，由该题引发出来一些问题，现在来总结下。

首先是二叉树的结构:

 struct TreeNode {
     EleType val;
     TreeNode *left;
     TreeNode *right;
 };

然后是二叉树，先序遍历的构建方法，由于只有扩展后的二叉树可以做到一个遍历序列确定一颗二叉树，比如图所示前序遍历序列(根左右)就为12#4##3##。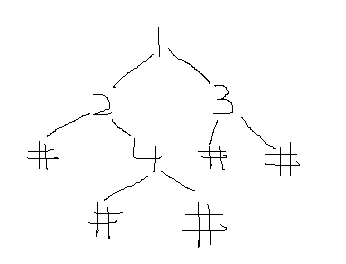

二叉树构建的代码，因为要对传递的值进行改变，所以不能值传递，所以注意这里的参数为指向TreeNode类型的指针的一个引用，

这是因为如果直接传递指针变量，给该函数的形参初始化之后，该形参在退出该函数就自动回收啦。

int CreateBiTree(TreeNode* &T)
{
    char data;
    //按先序次序输入二叉树中结点的值（一个字符），‘#’表示空树
    scanf("%c",&data);
    if(data == '#'){
        T = NULL;
    }
    else{
        T = (TreeNode*)malloc(sizeof(TreeNode));
        T->val = data;
        CreateBiTree(T->left);
        CreateBiTree(T->right);
    }
    return ;
} 

---

该题的思路：主要有递归和栈来实现两种方法。中心对称即左子树中某个节点的左孩子=对应的右子树的节点的右孩子，该节点的右孩子=对应结点的左孩子。

　　

代码：

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef int EleType;

 struct TreeNode {
     EleType val;
     TreeNode *left;
     TreeNode *right;
 };

class Solution {
public:
    bool check(TreeNode *leftNode, TreeNode *rightNode)
    {
        if (leftNode == NULL && rightNode == NULL)
            return true;

        if (leftNode == NULL || rightNode == NULL)
            return false;

        return leftNode->val == rightNode->val && check(leftNode->left, rightNode->right) &&
            check(leftNode->right, rightNode->left);
    }

    bool isSymmetric(TreeNode *root) {
        if (root == NULL)
            return true;
        return check(root->left, root->right);
    }
};

//按先序序列创建二叉树
int CreateBiTree(TreeNode* &T){
    int data;
    //按先序次序输入二叉树中结点的值（一个字符），‘#’表示空树
    cin>>data;
    if(data == -1){
        T = NULL;
    }
    else{
        T = (TreeNode*)malloc(sizeof(TreeNode));
        //生成根结点
        T->val = data;
        //构造左子树
        CreateBiTree(T->left);
        //构造右子树
        CreateBiTree(T->right);
    }
    return ;
} 

int main()
{
    freopen("C:\\Users\\Administrator\\Desktop\\test.txt","r",stdin);
    TreeNode* root=NULL;
    CreateBiTree(root);
    Solution so;
    cout<<so.isSymmetric(root)<<endl;
     return ;
}

ps:递归的终止条件：左节点和右节点都为空，则true；

左节点和右节点中只有一个不为空，返回false（因为上面的判断保证了肯定有一个不为空）