IE兼容rgba()透明度

一般浏览器的背景透明度可以直接设置

background:rgba(0,0,0,.5);

-webkit-background:rgba(0,0,0,.5);

-o-background:rgba(0,0,0,.5);

-moz-background:rgba(0,0,0,.5);

但是这在IE中是不支持的，所以有了以下的解决办法：

第一种：

-ms-background: #000;
filter: alpha(opacity=30);

第二种方法：

background: rgba(0, 0, 0, 0.5);
filter: progid:DXImageTransform.Microsoft.gradient(startcolorstr=#7f000000, endcolorstr=#7f000000);
设置filter属性目的是上一行的透明度不起作用的时候执行，
filter: progid:DXImageTransform.Microsoft.gradient是用来做渐变的，但是这个地方不需要渐变，所以两个颜色都设置成了相同的颜色。

这个颜色“#7f000000”是由两部分组成的。

第一部是#号后面的7f 。是rgba透明度0.5的IEfilter值。从0.1到0.9每个数字对应一个IEfilter值。对应关系如下：

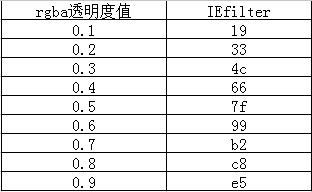
即：alpha*255得到的值再转换为16进制即可。

第二部分是7f后面的六位 是六进制的颜色值，跟rgb函数中的取值相同，比如rgb(255,255,255)对应#ffffff。