LeetCode刷题--有效的括号（简单）

题目描述

给定一个只包括 ' ( ' , ' )  '，  ' { ' , ' } ' ， ' [ ' , ' ] ' 的字符串，判断字符串是否有效。
有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。

• 左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

示例1：

输入："（）"
输出：true

示例2：

输入："（）[ ] { } "
输出：true

示例3：

输入："（ ] "
输出：false

示例4：

输入："（ [ ）] "
输出：false

示例5：

输入：" { [ ] } "
输出：true

简化版本

让我们看一下该问题的简化版本，在简化后的问题中，只含一种类型的括号。这么一来，我们将会遇到的表达式是

( ( ( ( ( ( ) ) ) ) ) )   - VALID
( ) ( ) ( ) ( )               -VALID
( ( ( ( ( ( ( ( )          -INVALID
( ( ( ) ( ( ) ) ) )       - VALID

我们试着用一个简单的算法来解决这一问题。

　　1. 我们从表达式的左侧开始，每次只处理一个括号。

　　2. 假设我们遇到一个开括号即（，表达式是否无效取决于这个表达式的其它部分是否有相匹配的闭括号即 ）。此时，我们只是增加计数器的值保持跟踪现在为止开括号的数目。left += 1 。

　　3. 如果我们遇到一个闭括号，这可能意味着这样两种情况：

　　　　·  此闭括号没有与之对应的开括号，在这种情况下，我们的表达式无效。当 left == 0，也就是没有未配对的左括号可用时就是这种情况。

　　　　·  我们有一些未配对的开括号可以与该闭括号配对。当1eft>0，也就是有未配对的左括号可用时就是这种情况。

　　4. 如果我们在 left == 0时遇到一个闭括号例如 ），那么当前的表达式无效。否则，我们会减少 left 的值，也就是减少了可用的未配对的左括号的数量。

　　5. 继续处理字符串，直到处理完所有括号。

　　6. 如果最后我们仍然有未配对的左括号，这意味着表达式无效。

在这里讨论这个特定算法是因为我们从该解决方案中获得灵感以解决原始问题。为了更好地理解我们讨论的算法，请观看下面的动画演示。

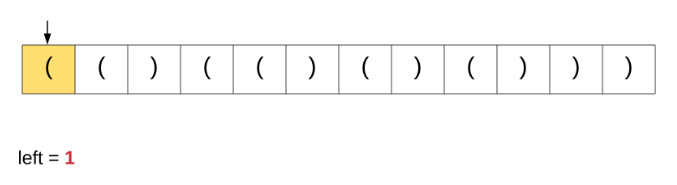
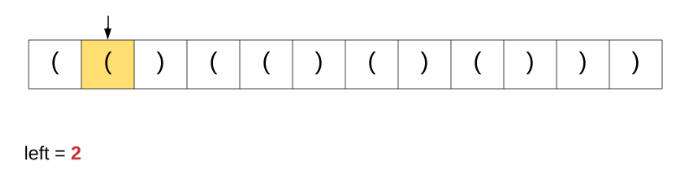
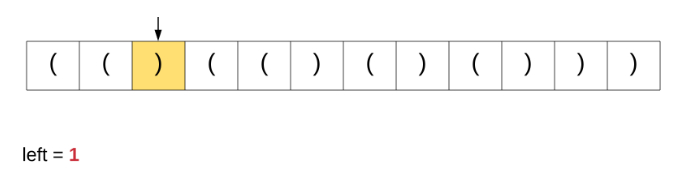
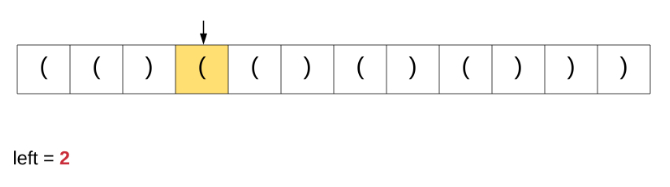
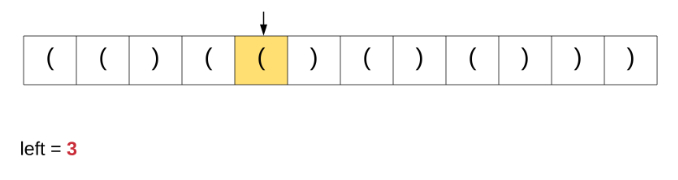
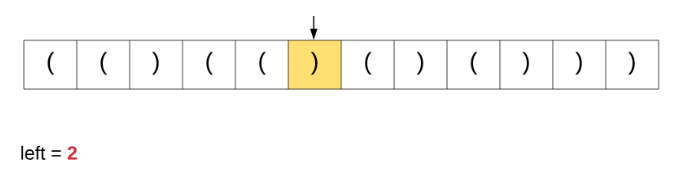
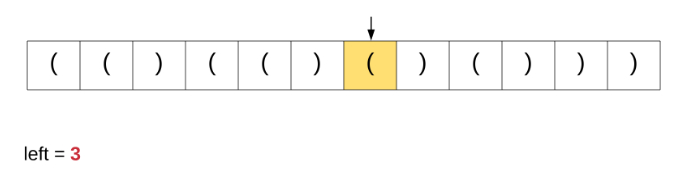
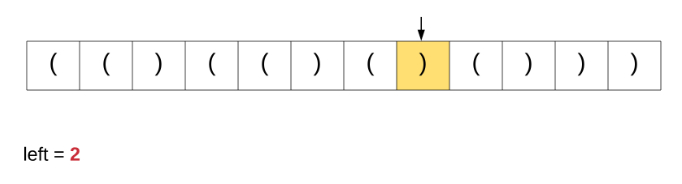
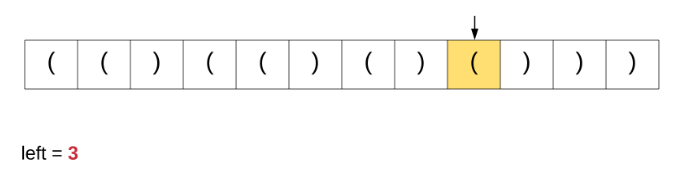
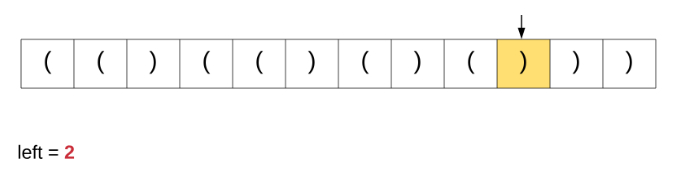
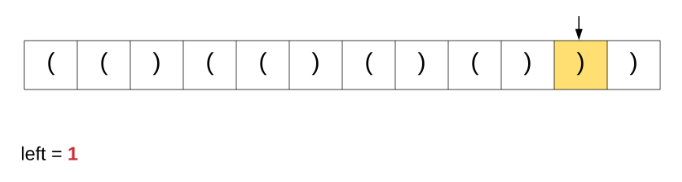
如果我们对原始问题这个办法，这是根本就行不通的。基于简单计数器的方法能够在上面完美运行是因为所有括号都具有相同的类型。

因此，当我们遇到一个闭括号时，我们只需要假设有一个对应匹配的开括号是可用的，即假设 left > 0。

但是，在我们的问题中，如果我们遇到 ]，我们真的不知道是否有相应的 [ 可用。你可能会问：

为什么不为不同类型的括号分别维护一个单独的计数器？

这可能不起作用，因为括号的相对位置在这里也很重要。例如：

[ { ]

如果我们只是在这里维持计数器，那么只要我们遇到闭合方括号，我们就会知道此处有一个可用的未配对的开口方括号。

但是，最近的未配对的开括号是一个花括号，而不是一个方括号，因此计数方法在这里被打破了。

方法一：栈

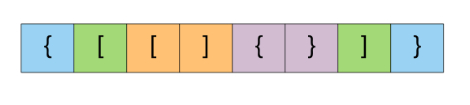
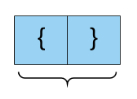
关于有效括号表达式的一个有趣属性是有效表达式的子表达式也应该是有效表达式。（不是每个子表达式）例如

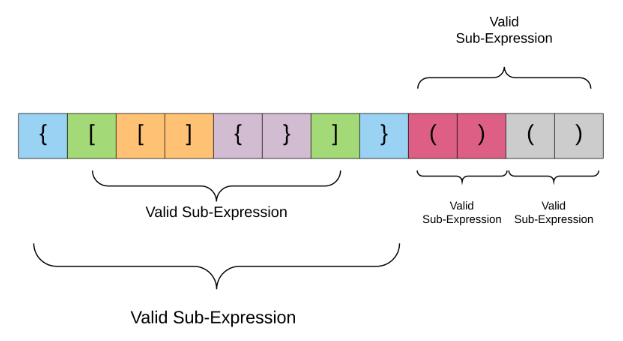
仔细查看上述结构，颜色标识的单元格将标记开闭的括号对。整个表达式是有效的，而它的子表达式本身也是有效的。这为问题提供了一种递归结构。例如，考虑上图中两个绿色括号内的表达式。开括号位于索引 1，相应闭括号位于索引 6。

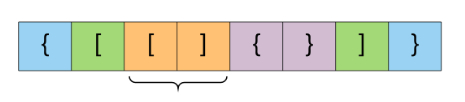
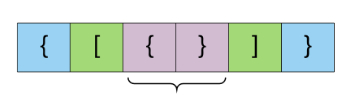
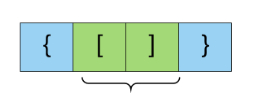
如果每当我们在表达式中遇到一对匹配的括号时，我们只是从表达式中删除它，会发生什么？

让我们看看下面的这个想法，从整体表达式中一次删除一个较小的表达式，因为这是一个有效的表达式，我们最后剩留下一个空字符串。

在表示问题的递归结构时，栈数据结构可以派上用场。我们无法真正地从内到外处理这个问题，因为我们对整体结构一无所知。但是，栈可以帮助我们递归地处理这种情况，即从外部到内部。

算法

　　1. 初始化栈S。

　　2. 依次处理表达式的每个括号，用一个栈来保存( ，[ , {

　　3.当遍历到这三个字符的时候，就将其保存到栈中。

　　4. 如果我们遇到一个闭括号，那么我们检查栈顶的元素。如果栈顶的元素是一个相同类型的左括号，那么我们将它从栈中弹出并继续处理。否则，这意味着表达式无效。

　　5. 如果到最后我们剩下的栈中仍然有元素，那么这意味着表达式无效。

我们来看一下该算法的动画演示，然后转到实现部分。

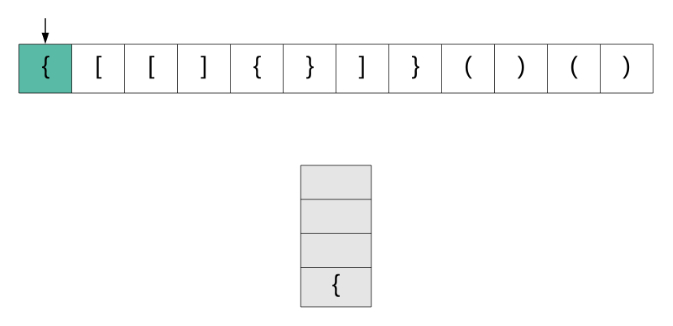
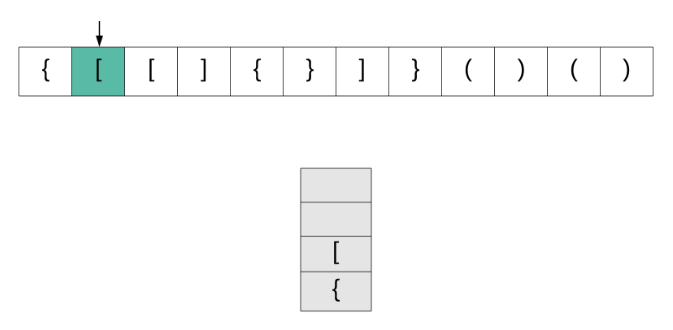
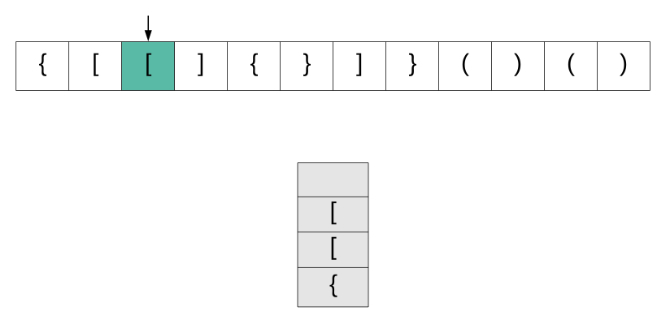
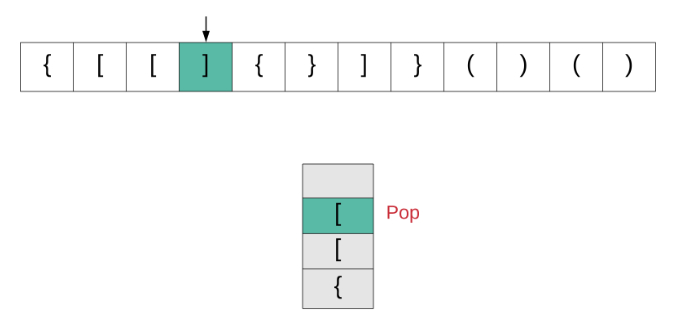
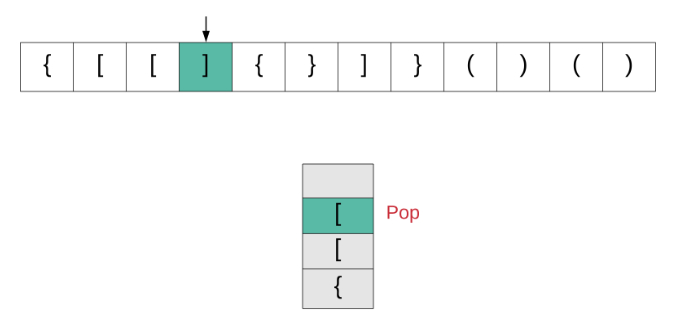
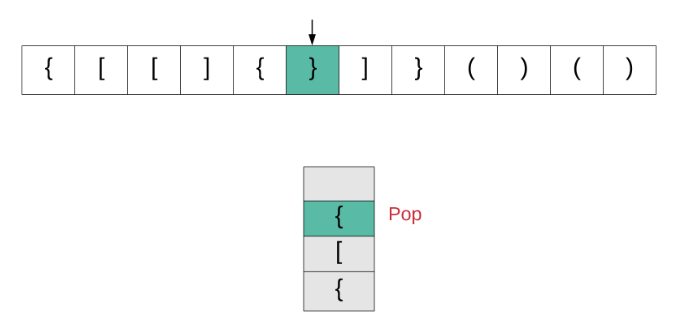
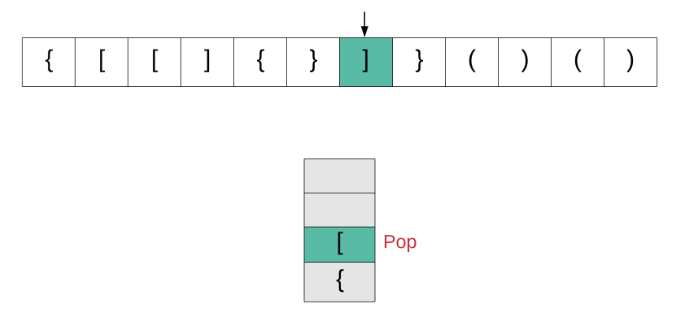
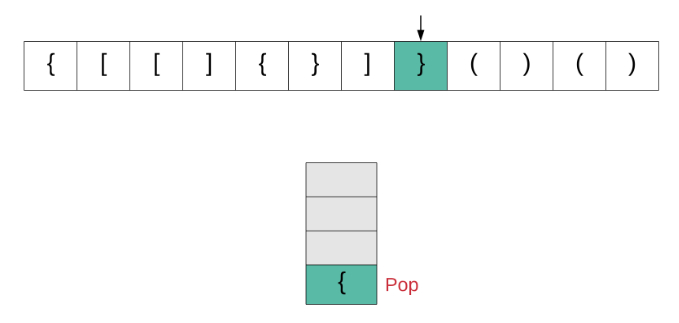
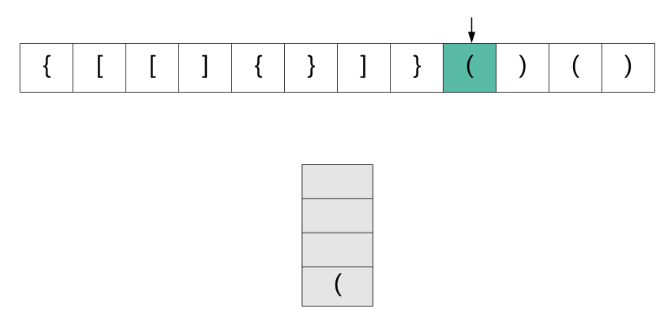
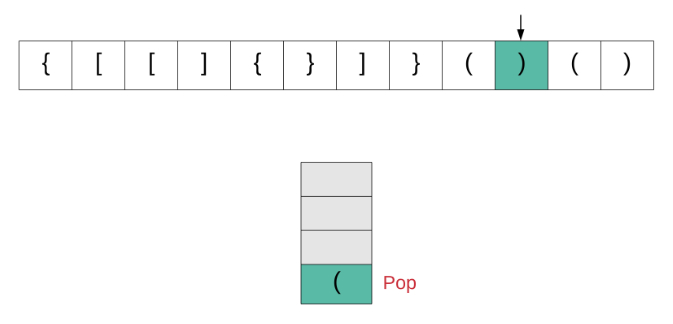
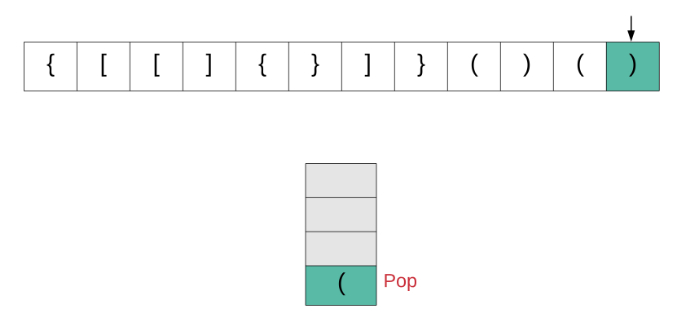
现在让我们看看该算法是如何实现的。

class Solution {
    public boolean isValid(String s) {
        if(s==null || "".equals(s)) {
            return true;
        }
        //用栈保存 (，[，{
        Stack<Character> stack = new Stack<Character>();
        //map中保存的是 ):(, ]:[,}:{
        //当遍历到 )时候就会去map中找对应的value，也就是(
        //再用这个value和stack弹出的元素比较，如果相等则匹配上，不等则返回false
        //这里也可以用数组来存，为了简单就用map表示了
        HashMap<Character,Character> map = new HashMap<Character,Character>();
        map.put(')','(');
        map.put(']','[');
        map.put('}','{');
        for(int i=0;i<s.length();i++) {
            char c = s.charAt(i);
            //如果map中不包含 (,[,{，就将这个字符放入栈中
            if(!map.containsKey(c)) {
                stack.add(c);
            } else {
                //如果遍历的字符不在map中，也就是说这个字符是),],}，那么就要跟栈中的元素比较
                //首先要判断栈是否为空，如果输入的字符是 )() ，那么当遍历到第一个)时，栈为空
                if(stack.size()==0) {
                    return false;
                }
                //取出栈顶的元素
                Character tmp = stack.pop();
                //假设当前遍历到的元素是 ]，那么从map中取到的value就是 [
                //如果栈顶的元素是 (，则不匹配返回false，否则继续
                if(map.get(c)!=tmp) {
                    return false;
                }
            }
        }
        //返回的时候还要判断栈是否为空
        //如果输入的字符串是 (((，那么最后栈就不为空
        return (stack.empty()? true : false);
    }
}