CF892D—Gluttony（思维，好题）

http://codeforces.com/contest/892/problem/D

D. Gluttony

You are given an array a with n distinct integers. Construct an array b by permuting a such that for every non-empty subset of indices S = {x₁, x₂, ..., x_k} (1 ≤ x_i ≤ n, 0 < k < n) the sums of elements on that positions in a and b are different, i. e.

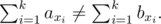
Input

The first line contains one integer n (1 ≤ n ≤ 22) — the size of the array.

The second line contains n space-separated distinct integers a₁, a₂, ..., a_n (0 ≤ a_i ≤ 10⁹) — the elements of the array.

Output

If there is no such array b, print -1.

Otherwise in the only line print n space-separated integers b₁, b₂, ..., b_n. Note that b must be a permutation of a.

If there are multiple answers, print any of them.

Examples

Input

2
1 2

Output

2 1 

Input

4
1000 100 10 1

Output

100 1 1000 10

Note

An array x is a permutation of y, if we can shuffle elements of y such that it will coincide with x.

Note that the empty subset and the subset containing all indices are not counted.

附上官方题解：

Sort the array and shift it by one. This array will be an answer.

Proof:

When we shift the sorted array all of the elements become greater except the first one, consider f = {1, 2, ..., n} and t = {x₁, x₂, ..., x_k} if 1 wasn't in t we would have

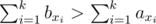
otherwise consider q = {y₁, y₂, ..., y_n - k} = f - t then 1 can't be in q and we have

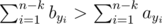
so

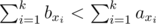
and we are done!

其实就是

把a序列做一个排序，设为c序列，然后我们开始构造b序列
b[i]=c[(j+1)%n]，满足c[j]=a[i]
例如：
a=[0,3,1,2]
那么
c=[0,1,2,3]
那么
b=[1,0,2,3]
b 就是我们要构造的序列

来自http://blog.csdn.net/weixin_37517391/article/details/78569584

证明：

若子集不包含最大数，则一定有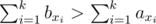

若子集包含最大数，则反过来考虑，其补集一定也有上面的式子成立，又因为n个数的sum相同，所以一定有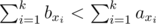（给定了序列中的数都是不同的条件）

证毕

代码：

  1 /*
  2 * @FileName: /media/shan/Study/代码与算法/2017训练比赛/11.17/d.cpp
  3 * @Author: Pic
  4 * @Created Time: 2017年11月17日 星期五 19时34分11秒
  5 */
  6 #include <bits/stdc++.h>
  7 using namespace std;
  8 const int maxn=30;
  9 int a[maxn];
 10 int b[maxn];
 11 int n;
 12 bool cmp(int a,int b)
 13 {
 14 	return a>b;
 15 }
 16 int fid(int x)
 17 {
 18 	for(int i=0;i<n;i++){
 19 		if(b[i]==x){
 20 			return i;
 21 		}
 22 	}
 23 }
 24 int main()
 25 {
 26 //	freopen("data.in","r",stdin);
 27 	//freopen("data.out","w",stdout);
 28 	cin>>n;
 29 	for(int i=0;i<n;i++){
 30 		cin>>a[i];
 31 		b[i]=a[i];
 32 	}
 33 	sort(b,b+n,cmp);
 34 	int index;
 35 	for(int i=0;i<n;i++){
 36 		index=fid(a[i]);
 37 		if(index==0){
 38 			cout<<b[n-1]<<" ";
 39 		}
 40 		else{
 41 			cout<<b[index-1]<<" ";
 42 		}
 43 	}
 44 	cout<<endl;
 45 }
 46