2019HDU多校第四场 Just an Old Puzzle ——八数码有解条件

理论基础

轮换与对换

概念：把 $S$ 中的元素 $i_1$ 变成 $i_2$，$i_2$ 变成 $i_3$ ... $i_k$ 又变成 $i_1$，并使 $S$ 中的其余元素保持不变的置换称为循环，又称轮换，记为 $(i_1, i_2,...,i_k)$，$k$ 称为循环长度，特别地，循环长度为2的循环称为对换。

定理：

（1）任一置换可表示成若干个无公共元素的循环之积

（2）任一置换可表示成若干个对换之积，且对换个数的奇偶性不变。

八数码中的置换

若一个置换可以分解成奇数个对换之积称为奇置换，否则称为偶置换.

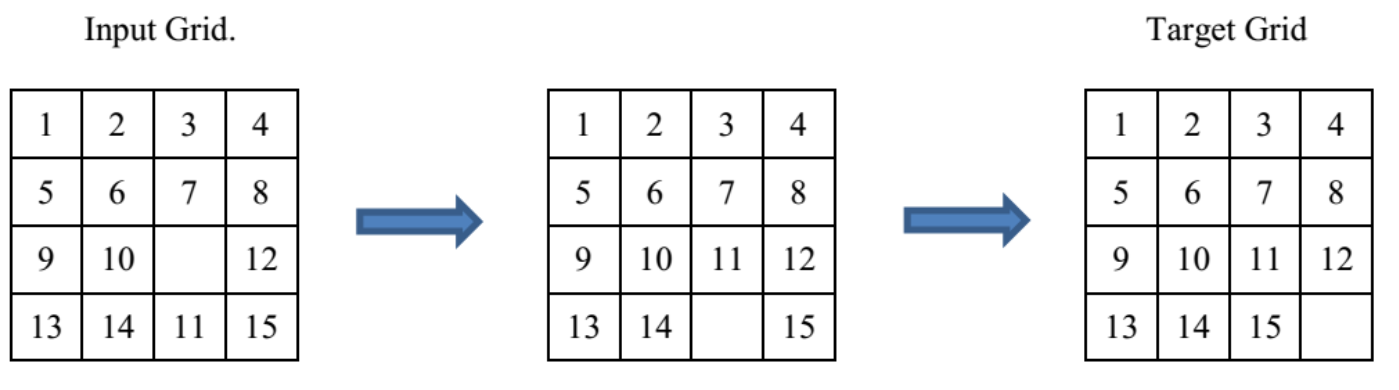
即进行如下置换：

$$\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 0 & 12 & 13 & 14 & 11 & 15\\
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 0
\end{pmatrix}$$

等价于轮换之积：

$\begin{pmatrix}
0 & 11 & 15\\
11 & 15 & 0
\end{pmatrix} = \left ( 0 \  11 \ 15\right ) = (0 \ 11)(0 \ 15)$

当置换的奇偶性与空格移动的奇偶性相同则有解，反之无解。

这是一个偶置换，而空格移动到右下角也是偶数步，所以是有解的。

然而，求两个状态的置换不方便实现，对换的奇偶性等价于逆序对奇偶性（gugu，我猜的）

逆序对

如果我们从上到下、从左到右展开成一维数组，某状态的奇偶性定义为逆序对(不包括0的)总数的奇偶性。

首先，空格的左右移动不会改变逆序对奇偶性

列数为奇数时，上下移动不改变奇偶性

列数为偶数时，上下移动奇偶取反。

大概的证明如下：

题目

由于是15数码，列数为偶数，且终态逆序对为偶数，所以只需 y%2=pair%2，y为空格到右下角的纵距离，pair为初始状态的逆序对数。

值得一提的是，题目有个120步的迷惑条件，维基百科有：十五数码的最优解至多80步，而八数码推盘的最优解至多31步。（数字推盘游戏）

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

const int maxn = ;
int a[maxn];

struct BIT{
    int C[maxn], n;
    void init(int n)
    {
        this->n = n;
        memset(C, , sizeof(C));
//        for (int i = 1; i <= n; i++)
//            add(i, a[i]);
    }
    int lowbit(int x)
    {
        return x & -x;
    }
    int sum(int x)
    {
        int ret = ;
        while (x > )
        {
            ret += C[x];
            x -= lowbit(x);
        }
        return ret;
    }
    void add(int x, int d)
    {
        while (x <= n)
        {
            C[x] += d;
            x += lowbit(x);
        }
    }
    int getPair()
    {
        int ret = ;
         for(int i = n;i >=;i--)
        {
            ret += sum(a[i] - );
            add(a[i], );
        }
        return ret;
    }
}bit;

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        int cnt = , y;
        for(int i =  ;i <= ;i++)
        {
            int tmp;
            scanf("%d", &tmp);
            if(!tmp)  y =  - (i-)/;
            else  a[++cnt] = tmp;
        }
        bit.init(cnt);  //printf("%d %d %d\n", bit.n,  bit.getPair(), y);
        if(y% == bit.getPair()%)  printf("Yes\n");
        else  printf("No\n");
    }

    return ;
}

参考链接：http://www.voidcn.com/article/p-wsmvxpvl-bbo.html