怎样求控制器的增益系数k？

步骤：

1.  \dot x =A*x + B*u is a state space model, with A and B are known. Now we want to locate the poles p at the desired location, so need the help with designing a controller: u= - k*x。How to choose the gain k?

Answer: Substituting u= - k*x, then \dot = (A-B*K)x, use place function in Matlab to input (A,B,p), obtaining k from the output.

About the introduction of place function, I attach a paragraph from Wikipedia here:

Description

Given the single- or multi-input system

˙x=Ax+Bu

and a vector p of desired self-conjugate closed-loop pole locations, place computes a gain matrix K such that the state feedback u = –Kx places the closed-loop poles at the locations p. In other words, the eigenvalues of A – BK match the entries of p (up to the ordering).

K = place(A,B,p) places the desired closed-loop poles p by computing a state-feedback gain matrix K. All the inputs of the plant are assumed to be control inputs. The length of p must match the row size of A. place works for multi-input systems and is based on the algorithm from [1]. This algorithm uses the extra degrees of freedom to find a solution that minimizes the sensitivity of the closed-loop poles to perturbations in A or B.

[K,prec,message] = place(A,B,p) returns prec, an estimate of how closely the eigenvalues of A – BK match the specified locations p (prec measures the number of accurate decimal digits in the actual closed-loop poles). If some nonzero closed-loop pole is more than 10% off from the desired location, message contains a warning message.

You can also use place for estimator gain selection by transposing the A matrix and substituting C' for B.

l = place(A',C',p).'

Examples

Pole Placement Design

Consider a state-space system (a,b,c,d) with two inputs, three outputs, and three states. You can compute the feedback gain matrix needed to place the closed-loop poles at p = [-1 -1.23 -5.0] by

p = [-1 -1.23 -5.0];
K = place(a,b,p)

2. How to design the desired poles? Answer: Choose a suitable value of \omega (bandwith) and \zeta (damping) of the controlling system:

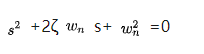
Then use the roots function to input the \omega and \zeta, obtaining the roots (the poles)  as the output.

About the introduction of roots function, I attach a paragraph from Wikipedia here:

The roots function calculates the roots of a single-variable polynomial represented by a vector of coefficients.

For example, create a vector to represent the polynomial x²−x−6, then calculate the roots.

p = [1 -1 -6];
r = roots(p)

r =

     3
    -2

Then with poles and system matrix (A, B), we can calculate the gain k.