EM算法分析

参考来源：

1. 《机器学习》——周志华
2. https://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html

几个概念

• 极大似然估计

A事件发生了，A与某因素θ有关，我们“理所当然”认为θ的取值应该使A发生的概率最大，即θ的极大似然估计为θ=arg max_θ P(A|θ)

• Jensen不等式

对于下凸函数f和变量X，有不等式：E[f(X)]>=f(E[X])

上式易从函数的几何形状推出。

EM算法

EM算法即Expectation-Maximization，期望最大化算法。

其基本想法为：若参数θ已知，则可根据训练集推断最优隐变量Z（E步）；若Z已知，则可对θ做极大似然估计，调整θ。

假设有变量X及隐变量Z，参数为θ，则对θ做极大似然估计：

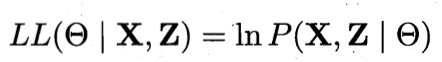
由于Z为隐变量，无法直接求解上式，此时可对Z计算期望，来最大化X的对数边际似然：

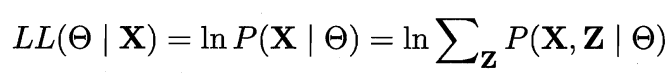
EM算法以初始θ为起点，通过以下操作迭代至收敛。

EM算法原型：

1. 基于θ_t推断隐变量Z的期望Z_t
2. 基于变量X和Z_t对参数θ做极大似然估计，得到θ_t+1

若不取Z的期望，而是根据θ计算Z的概率分布P(Z|X,θ)，则：

• 以当前参数θ_t推断Z的分布，并计算对数似然LL(θ|X,Z)关于Z的期望

• 
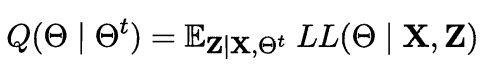
• 寻找参数最大化期望似然，即
• 

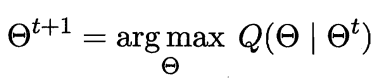
下面，我们基于概率分布进行具体推导：

θ的对数似然为：

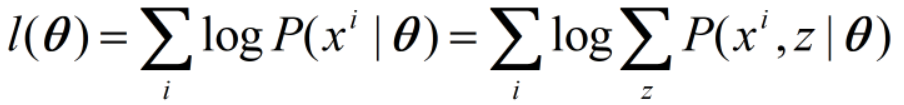
我们变形一下，并应用上面的不等式：

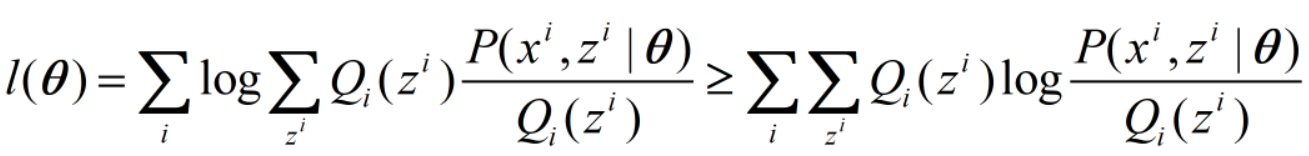
上式推导过程为：

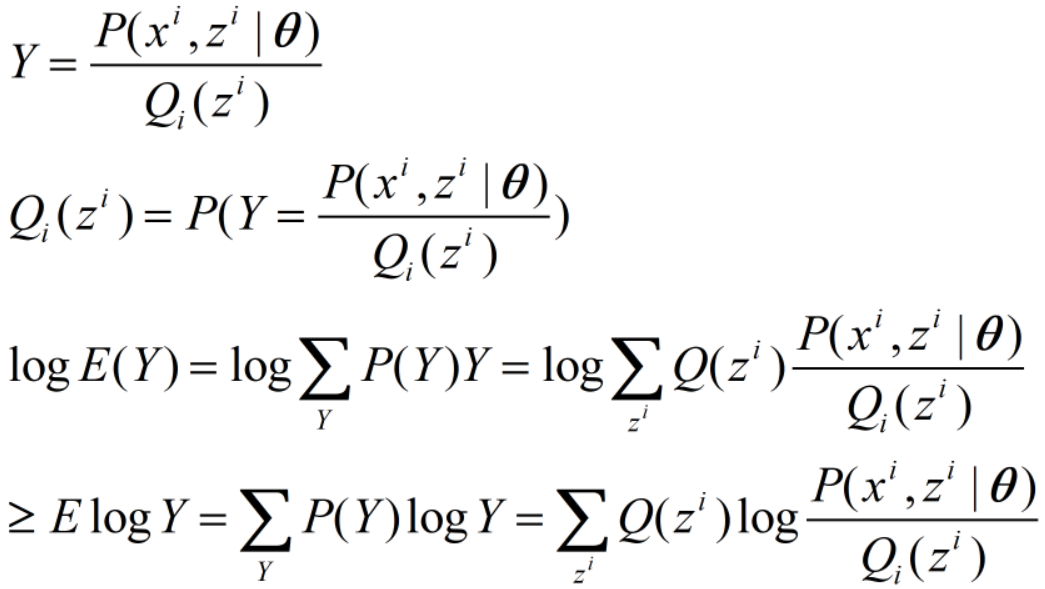
不等式取等号当且仅当变量为常数c，即

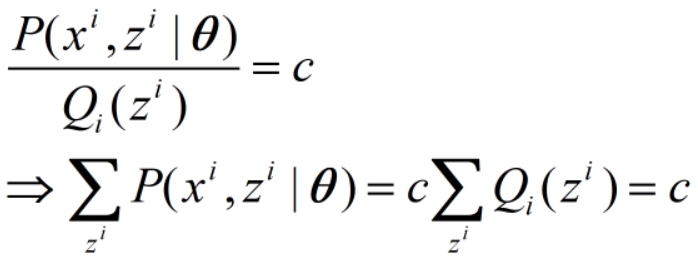
则Q(z)为：

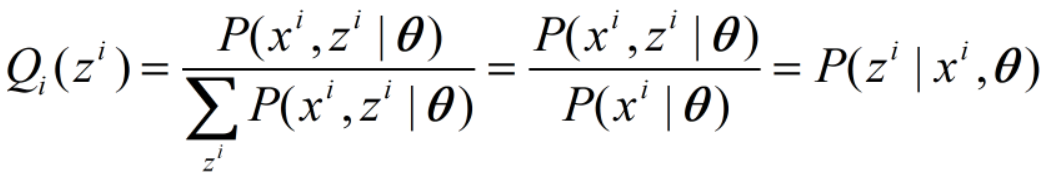
此即E步更新。

固定Q(z)，更新参数，即M步为：

由于

去掉常数项，参数的更新即为：

至此，推导结束。E和M步迭代进行，至似然不再变化或变化小于阈值停止。

EM算法的几何解释

E步相当于使下界函数抬高至不等式取等号处，M步相当于调整参数使下界函数取得极大值，此时更新参数应该会改变下界函数，然后继续执行E、M步。

另外，EM算法只保证收敛到局部最优（对于凸函数，只有一个极值，当然就是全局最优）。