超详细的EM算法理解

众所周知，极大似然估计是一种应用很广泛的参数估计方法。例如我手头有一些东北人的身高的数据，又知道身高的概率模型是高斯分布，那么利用极大化似然函数的方法可以估计出高斯分布的两个参数，均值和方差。这个方法基本上所有概率课本上都会讲，我这就不多说了，不清楚的请百度。

　　然而现在我面临的是这种情况，我手上的数据是四川人和东北人的身高合集，然而对于其中具体的每一个数据，并没有标定出它来自“东北人”还是“四川人”，我想如果把这个数据集的概率密度画出来，大约是这个样子：

　　

　　好了不要吐槽了，能画成这个样子我已经很用心了= =

　　其实这个双峰的概率密度函数是有模型的，称作高斯混合模型（GMM），写作：

　　

　　话说往博客上加公式真是费劲= =这模型很好理解，就是k个高斯模型加权组成，α是各高斯分布的权重，Θ是参数。对GMM模型的参数估计，就要用EM算法。更一般的讲，EM算法适用于带有隐变量的概率模型的估计，什么是隐变量呢？就是观测不到的变量，对于上面四川人和东北人的例子，对每一个身高而言，它来自四川还是东北，就是一个隐变量。

　　为什么要用EM，我们来具体考虑一下上面这个问题。如果使用极大似然估计——这是我们最开始最单纯的想法，那么我们需要极大化的似然函数应该是这个：

　　

　　然而我们并不知道p(x;θ)的表达式，有同学说我知道啊，不就是上面那个混个高斯模型？不就是参数多一点麽。

　　仔细想想，GMM里的θ可是由四川人和东北人两部分组成哟，假如你要估计四川人的身高均值，直接用GMM做似然函数，会把四川人和东北人全考虑进去，显然不合适。

　　另一个想法是考虑隐变量，如果我们已经知道哪些样本来自四川，哪些样本来自东北，那就好了。用Z=0或Z=1标记样本来自哪个总体，则Z就是隐变量，需要最大化的似然函数就变为：

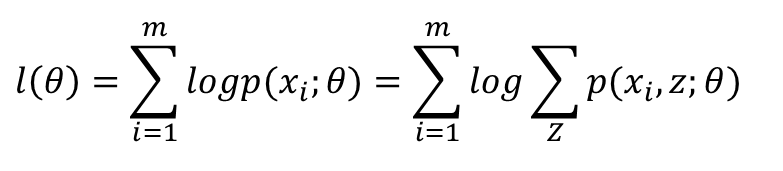
　　然而并没有卵用，因为隐变量确实不知道。要估计一个样本是来自四川还是东北，我们就要有模型参数，要估计模型参数，我们首先要知道一个样本是来自四川或东北的可能性...

　　到底是鸡生蛋，还是蛋生鸡？

　　不闹了，我们的方法是假设。首先假设一个模型参数θ，然后每个样本来自四川/东北的概率p(z_i)就能算出来了，p(x_i,z_i)=p(x_i|z_i)p(z_i)，而x|z=0服从四川人分布，x|z=1服从东北人分布，所以似然函数可以写成含有θ的函数，极大化它我们可以得到一个新的θ。新的θ因为考虑了样本来自哪个分布，会比原来的更能反应数据规律。有了这个更好的θ我们再对每个样本重新计算它来自四川和东北的概率，用更好的θ算出来的概率会更准确，有了更准确的信息，我们可以继续像上面一样估计θ，自然而然这次得到的θ会比上一次更棒，如此蒸蒸日上，直到收敛（参数变动不明显了），理论上，EM算法就说完了。

　　然而事情并没有这么简单，上面的思想理论上可行，实践起来不成。主要是因为似然函数有“和的log”这一项，log里面是一个和的形式，一求导这画面不要太美，直接强来你要面对 “两个正态分布的概率密度函数相加”做分母，“两个正态分布分别求导再相加”做分子的分数形式。m个这玩意加起来令它等于0，要求出关于θ的解析解，你对自己的数学水平想的不要太高。

　　怎么办？先介绍一个不等式，叫Jensen不等式，是这样说的：

　　X是一个随机变量，f(X)是一个凸函数（二阶导数大或等于0），那么有：

　　

　　当且仅当X是常数的时候等号成立

　　如果f（X）是凹函数，不等号反向

　　关于这个不等式，我既不打算证明，也不打算说明，希望你承认它正确就好。

　　半路杀出一个Jensen不等式，要用它解决上面的困境也是应有之义，不然说它做什么。直接最大化似然函数做不到，那么如果我们能找到似然函数的一个紧的下界一直优化它，并保证每次迭代能够使总的似然函数一直增大，其实也是一样的。怎么说？画个图你就明白了：

　　

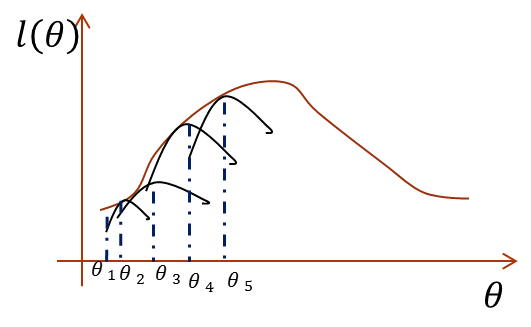
　　图画的不好，多见谅。横坐标是参数，纵坐标是似然函数，首先我们初始化一个θ1，根据它求似然函数一个紧的下界，也就是图中第一条黑短线，黑短线上的值虽然都小于似然函数的值，但至少有一点可以满足等号（所以称为紧下界），最大化小黑短线我们就hit到至少与似然函数刚好相等的位置，对应的横坐标就是我们的新的θ2，如此进行，只要保证随着θ的更新，每次最大化的小黑短线值都比上次的更大，那么算法收敛，最后就能最大化到似然函数的极大值处。

　　构造这个小黑短线，就要靠Jensen不等式。注意我们这里的log函数是个凹函数，所以我们使用的Jensen不等式的凹函数版本。根据Jensen函数，需要把log里面的东西写成一个数学期望的形式，注意到log里的和是关于隐变量Z的和，于是自然而然，这个数学期望一定是和Z有关，如果设Q(z)是Z的分布函数，那么可以这样构造：

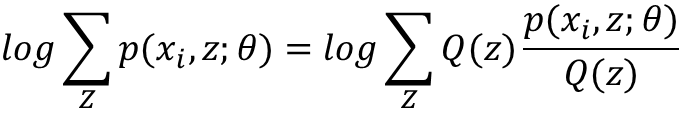
　　这几句公式比较多，我不一一敲了，直接把我PPT里的内容截图过来：

　　

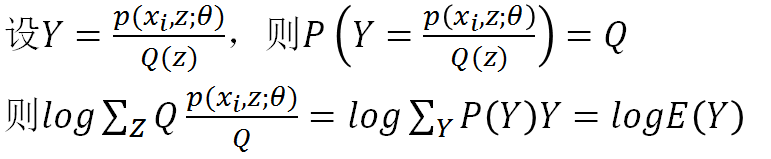
　　所以log里其实构造了一个随机变量Y，Y是Z的函数，Y取p/Q的值的概率是Q，这点说的很清楚了。

　　构造好数学期望，下一步根据Jensen不等式进行放缩：

　　

　　有了这一步，我们看一下整个式子：

　　

　　也就是说我们找到了似然函数的一个下界，那么优化它是否就可以呢？不是的，上面说了必须保证这个下界是紧的，也就是至少有点能使等号成立。由Jensen不等式，等式成立的条件是随机变量是常数，具体到这里，就是：

　　　　

　　又因为Q（z）是z的分布函数，所以：

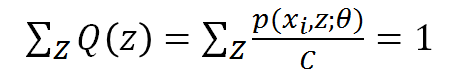
　　把C乘过去，可得C就是p(xi,z)对z求和，所以我们终于知道了：

　　

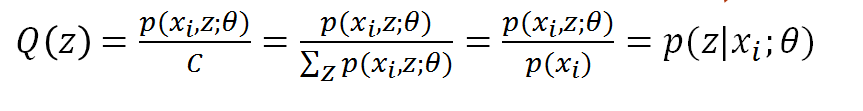
_{得到Q(z)，大功告成，Q(z)就是p(zi|xi)，或者写成p(zi)，都是一回事，代表第i个数据是来自zi的概率。}

　　于是EM算法出炉，它是这样做的：

　　首先，初始化参数θ

　　（1）E-Step：根据参数θ计算每个样本属于zi的概率，即这个身高来自四川或东北的概率，这个概率就是Q

　　（2）M-Step：根据计算得到的Q，求出含有θ的似然函数的下界并最大化它，得到新的参数θ

　　重复（1）和（2）直到收敛，可以看到，从思想上来说，和最开始没什么两样，只不过直接最大化似然函数不好做，曲线救国而已。

　　至于为什么这样的迭代会保证似然函数单调不减，即EM算法的收敛性证明，我就先不写了，以后有时间再考虑补。需要额外说明的是，EM算法在一般情况是收敛的，但是不保证收敛到全局最优，即有可能进入局部的最优。EM算法在混合高斯模型，隐马尔科夫模型中都有应用，是著名的数据挖掘十大算法之一。

转自：https://www.cnblogs.com/bigmoyan/p/4550375.html