Deep Learning专栏--FFM+Recurrent Entity Network的端到端方案

很久没有写总结了，这篇博客仅作为最近的一些尝试内容，记录一些心得。FFM的优势是可以处理高维稀疏样本的特征组合，已经在无数的CTR预估比赛和工业界中广泛应用，此外，其也可以与Deep Networks结合（如DeepFM等工作），很好地应用在数据规模足够大的工业场景中。Recurrent Entity Network是facebook AI在2017年的ICLR会议上发表的，文章提出了Recurrent Entity Network的模型用来对world state进行建模，根据模型的输入对记忆单元进行实时的更新，从而得到对world的一个即时的认识。该模型可以用于机器阅读理解、QA等领域。

如果我们希望做一个关于豆瓣电影的QA机器人，我们有每个电影的剧情文本介绍和豆瓣下面的评论，也有每个电影的特征（如其导演、演员、获奖情况、拍摄年份等），那么利用FFM对电影特征进行Embedding向量化，再利用Deep Networks对电影剧情文本和评论文本进行向量化，两者融合起来，岂不是可以更好地回答提问者的问题？而Entity Networks通过memory机制存储文本上下文信息，能够更好地捕获前后信息，抓住实体关系，在QA领域会更加游刃有余。

1. 从线性模型到FFM

1.1 线性模型

常见的线性模型，比如线性回归、逻辑回归等，它只考虑了每个特征对结果的单独影响，而没有考虑特征间的组合对结果的影响。

对于一个有n维特征的模型，线性回归的形式如下：

$$  f(x) = \omega_0 + \omega_1x_1+\omega_2x_2+...+\omega_nx_n =\omega_0+\sum_{i=1}^n{\omega_ix_i} \tag{1}  $$

其中$(\omega_0,\omega_1...\omega_n)$为模型参数，$(x_1,x_2...x_n)$为特征。
从(1)式可以看出来，模型的最终计算结果是各个特征的独立计算结果，并没有考虑特征之间的相互关系。
举个例子，我们“USA”与”Thanksgiving”，”China”与“Chinese new year”这样的组合特征是很有意义的，在这样的组合特征下，会对某些商品表现出更强的购买意愿，而单独考虑国家及节日都是没有意义的。

1.2 二项式模型

我们在（1）式的基础上，考虑任意2个特征分量之间的关系，得出以下模型：

$$ f(x)=\omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n\omega_{ij}x_ix_j \tag{2} $$

这个模型考虑了任意2个特征分量之间的关系，但并未考虑更高阶的关系。 
模型涉及的参数数量为：

$$ 1+n+\frac{n(n-1)}{2}=\frac{1}{2}(n^2+n+2) \tag{3} $$

对于参数$\omega_i$的训练，只要这个样本中对应的$x_i$不为0，则可以完成一次训练。
但对于参数$\omega_{ij}$的训练，需要这个样本中的$x_i$和$x_j$同时不为0，才可以完成一次训练。
在数据稀疏的实际应用场景中，二次项$\omega_{ij}$的训练是非常困难的。因为每个$\omega_{ij}$都需要大量$x_i$和$x_j$都不为0的样本。但在数据稀疏性比较明显的样本中，$x_i$和$x_j$都不为0的样本会非常稀少，这会导致$\omega_{ij}$不能得到足够的训练，从而不准确。

1.3 FM算法

1.3.1 FM基本原理

为了解决上述由于数据稀疏引起的训练不足的问题，我们为每个特征维度$x_i$引入一个辅助向量：

$$ V_i = (v_{i1},v_{i2},v_{i3},...,v_{ik})^T\in \mathbb R^k, i=1,2,3,...,n \tag{4} $$

其中$k$为辅助变量的维度，依经验而定，一般而言，对于特征维度足够多的样本，$k<<n$。

1.3.2 模型及目标函数

目标是要求得以下交互矩阵W：

$$ W=
\begin{pmatrix}
\omega_{11} & \omega_{12}& ... &\omega_{1n} \\
\omega_{21} & \omega_{22}& ... &\omega_{2n} \\
\vdots &\vdots &\ddots &\vdots\\
\omega_{n1} & \omega_{n2}& ... &\omega_{nn} \\
\end{pmatrix}_{n\times n}\tag{7}$$

由于直接求解W不方便，因此我们引入隐变量V：

$$ V=
\begin{pmatrix}
v_{11} & v_{12}& ... &v_{1k} \\
v_{21} & v_{22}& ... &v_{2k} \\
\vdots &\vdots &\ddots &\vdots\\
v_{n1} & v_{n2}& ... &v_{nk} \\
\end{pmatrix}_{n\times k}=\begin{pmatrix}
V_1^T\\
V_2^T\\
\cdots \\
V_n^T\\
\end{pmatrix}\tag{8}$$

令

$$ VV^T = W\tag{9}$$

如果我们先得到V，则可以得到W了。
现在只剩下一个问题了，是否一个存在V，使得上述式（9）成立。
理论研究表明：当k足够大时，对于任意对称正定的实矩阵$W\in \mathbb R^{n \times  n}$，均存在实矩阵$V\in \mathbb R^{n \times  k}$，使得$W=VV^T$。
理论分析中要求参数k足够的大，但在高度稀疏数据的场景中，由于 没有足够的样本，因此k通常取较小的值。事实上，对参数k的限制，在一定程度上可以提高模型的泛化能力。

假设样本中有n个特征，每个特征对应的隐变量维度为k，则参数个数为1+n+nk。 
正如上面所言，对于特征维度足够多的样本，$k<<n$。

根据以上参数，列出FM的目标函数：

$$ f(x) = \omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(V_i^TV_j)x_ix_j \tag{6}  $$

1.3.3 计算梯度

FM有一个重要的性质：multilinearity。若记$\Theta=(\omega_0,\omega_1,\omega_2,...,\omega_n,v_{11},v_{12},...,v_{nk})$表示FM模型的所有参数，则对于任意的$\theta \in \Theta$，存在与$\theta$无关的$g(x)$与$h(x)$，使得式（6）可以表示为：

$$ f(x) = g(x) + \theta h(x) \tag{11} $$

从式（11）中可以看出，如果我们得到了$g(x)$与$h(x)$，则对于参数$\theta$的梯度为$h(x)$。下面我们分情况讨论。

A. 当$\theta=\omega_0$时，式（6）可以表示为：

$$ f(x) = \color{blue}{\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(V_i^TV_j)x_ix_j} +\omega_0 \times \color{red}{1}\tag{12} $$

上述中的蓝色表示$g(x)$，红色表示$h(x)$。下同。

从上述式子可以看出此时的梯度为1.

B. 当$\theta=\omega_l, l \in (1,2,...,n)$时，

$$ f(x) = \color{blue}{\omega_0+\sum_{\substack{i=1 \\ i \ne l}}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(V_i^TV_j)x_ix_j}+\omega_l \times \color{red}{x_l} \tag{13} $$

此时梯度为$x_l$。

C. 当$\theta=v_{lm}$时，

$$ f(x) =\color{blue}{ \omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^n(\sum_{\substack{s=1 \\ is \ne lm \\js \ne lm}}^k v_{is}v_{js})x_ix_j }+v_{lm}\times \color{red}{x_l\sum_{\substack{i=1\\i \ne l }}^n v_{im}x_i} \tag{14}$$

此时梯度为$x_l\sum_{i \ne l } v_{im}x_i$。

综合上述结论，$f(x)$关于$\theta $的偏导数为：

$$ \frac{\partial f(x)}{\partial \theta} =
\begin{cases}
1, & \theta=\omega_0 \\
x_l, & \theta=\omega_l, l \in (1,2,...,n) \\
x_l\sum_{\substack{i=1\\i \ne l }}^n v_{im}x_i & \theta=v_{lm}
\end{cases} \tag{15}$$

1.3.4 时间复杂度

对于模型的计算时间复杂度，由（6）式，有：

$$ \begin{array}{l}
\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^n {(V_i^T{V_j})} } {x_i}{x_j}
\\= \frac{1}{2}\left( {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {(V_i^T{V_j})} } {x_i}{x_j} - \sum\limits_{i = 1}^n {(V_i^T{V_i})} {x_i}{x_i}} \right)
\\= \frac{1}{2}\left( {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\sum\limits_{l = 1}^k {{v_{il}}} } } {v_{jl}}{x_i}{x_j} - \sum\limits_{i = 1}^n {\sum\limits_{l = 1}^k {v_{il}^2} } x_i^2} \right)
\\= \frac{1}{2}\sum\limits_{l = 1}^k {\left( {\sum\limits_{i = 1}^n {({v_{il}}{x_i})} \sum\limits_{j = 1}^n {({v_{jl}}{x_j})} - \sum\limits_{i = 1}^n {v_{il}^2} x_i^2} \right)}
\\= \frac{1}{2}\sum\limits_{l = 1}^k {\left( {{{\left( {\sum\limits_{i = 1}^n {({v_{il}}{x_i})} } \right)}^2} - \sum\limits_{i = 1}^n {v_{il}^2} x_i^2} \right)}
\end{array} \tag{10} $$

上述式子中的$\sum\limits_{i = 1}^n {({v_{il}}{x_i})}$只需要计算一次就好，因此，可以看出上述模型的复杂度为$O(kn)$。
也就是说我们不要直接使用式（6）来计算预测结果，而应该使用式（10），这样的计算效率更高。

对于训练时间复杂度，由式（15）可以得到，

$$ x_l\sum_{\substack{i=1\\i \ne l }}^n v_{im}x_i = x_l\sum_{i=1}^n v_{im}x_i-v_{lm}x_l^2 \tag{16} $$

对于上式中的前半部分$\sum_{i=1}^n v_{im}x_i$，对于每个样本只需要计算一次，所以时间复杂度为$O(n)$，对于k个隐变量的维度分别计算一次，则复杂度为$O(kn)$。其它项的时间复杂度都小于这一项，因此，模型训练的时间复杂度为$O(kn)$。

具体地解释，

（1）我们首先计算$\sum_{i=1}^n v_{im}x_i$，时间复杂度为n，这个值对于所有特征对应的隐变量的某一个维度是相同的。我们设这值为C。
（2）计算每一个特征对应的$x_l\sum_{i=1}^n v_{im}x_i-v_{lm}x_l^2 =Cx_l-v_{lm}x_l^2$，由于总共有n个特征，因此时间复杂度为n，至此，总的时间复杂度为n+n。
（3）上述只是计算了隐变量的其中一个维度，我们总共有k个维度，因此总的时间复杂度为$k(n+n)=O(kn)k(n+n)=O(kn)$.

1.4 FFM算法

1.4.1 FFM基本原理

在FM模型中，每一个特征会对应一个隐变量，但在FFM模型中，认为应该将特征分为多个field，每个特征对应每个field分别有一个隐变量。

举个例子，我们的样本有3种类型的字段：publisher, advertiser, gender，分别可以代表媒体，广告主或者是具体的商品，性别。其中publisher有5种数据，advertiser有10种数据，gender有男女2种，经过one-hot编码以后，每个样本有17个特征，其中只有3个特征非空。

如果使用FM模型，则17个特征，每个特征对应一个隐变量。
如果使用FFM模型，则17个特征，每个特征对应3个隐变量，即每个类型对应一个隐变量，具体而言，就是对应publisher, advertiser, gender三个field各有一个隐变量。

1.4.2 模型及目标函数

根据上面的描述，可以得出FFM的模型为：

$$ f(x) = \omega_0+\sum_{i=1}^n\omega_ix_i+\sum_{j1=1}^{n-1}\sum_{j2=i+1}^n(V_{j1,f2}^TV_{j2,f1})x_{j1}x_{j2} \tag{17}$$

其中$j1, j2$表示特征的索引。我们假设$j1$特征属于$f1$这个field，$j2$特征属于$f2$这个field，则$V_{j1,f2}$表示$j1$这个特征对应$f2$($j2$所属的field)的隐变量，同时$V_{j2,f1}$表示$j2$这个特征对应$f1$($j1$所属的field)的隐变量。

事实上，在大多数情况下，FFM模型只保留了二次项，即：

$$ \phi(V,x) = \sum_{j1=1}^{n-1}\sum_{j2=i+1}^n(V_{j1,f2}^TV_{j2,f1})x_{j1}x_{j2} \tag{18} $$

根据逻辑回归的损失函数及分析，可以得出FFM的最优化问题为：

$$ \min \frac{\lambda}{2}||V||_2^2+\sum_{i=1}^{m}\log(1+exp(-y_i\phi(V,x))) \tag{19} $$

上面加号的前面部分使用了L2范式，后面部分是逻辑回归的损失函数。m表示样本的数量，yiyi表示训练样本的真实值（如是否点击的-1/1），$\phi(V,x)$表示使用当前的V代入式（18）计算得到的值。

注意，以上的损失函数适用于样本分布为{-1,1}的情况。

1.4.3 完整算法流程

与FTRL一样，FFM也使用了累积梯度作为自适应学习率的一部分，即：

$$ V_{j1,f2} = V_{j1,f2} - \frac{\eta}{\sqrt{1+\sum_t(g_{v_{j1,f2}}^t)^2}}g_{v_{j1,f2}} \tag{20} $$

其中$g_{v_{j1,f2}}$表示对于$V_{v_{j1,f2}}$这个变量的梯度向量，因为$V_{v_{j1,f2}}$是一个向量，因此$g_{v_{j1,f2}}$也是一个向量，尺寸为隐变量的维度大小，即k。
而$\sum_t(g_{v_{j1,f2}}^t)^2$表示从第一个样本到当前样本一直以来的累积梯度平方和。

$$ (V_{j1,f2})_d=(V_{j1,f2})_{d-1}-\frac{\eta}{\sqrt{(G_{j1,f2})_d}} \cdot (g_{j1,f2})_d\\
(V_{j2,f1})_d=(V_{j2,f1})_{d-1}-\frac{\eta}{\sqrt{(G_{j2,f1})_d}} \cdot (g_{j2,f1})_d \tag{21} $$

其中$G$为累积梯度平方和：

$$ (G_{j1,f2})_d=(G_{j1,f2})_{d-1}+(g_{j1,f2})_d^2 \\
(G_{j2,f1})_d=(G_{j2,f1})_{d-1}+(g_{j2,f1})_d^2 \tag{22} $$

$g$为梯度，比如$g_{ji,f2}$为$j1$这个特征对应$f2$这个field的梯度向量：

$$ g_{ji,f2}=\lambda \cdot V_{ji,f2} + \kappa \cdot V_{j2,f1}\\
g_{j2,f1}=\lambda \cdot V_{j2,f1} + \kappa \cdot V_{j1,f2} \tag{23} $$

其中$\kappa$为：

$$ \kappa = \frac{{\partial \log (1 + exp( - {y_i}\phi (V,x)))}}{{\partial \phi (V,x)}} = \frac{{ - y}}{{1 + \exp (y\phi (V,x))}} \tag{24} $$

$g$与$V$都是$k$维的向量，在python中可以作为一个向量计算，在java/c++等需要通过一个循环进行计算。

详细推导（23）式如下：
（1）在SGD中，式（19）可以转化为：

$$ \min \frac{\lambda}{2}||V||_2^2+\log(1+exp(-y_i\phi(V,x))) \tag{25} $$

（2）上式对$V_{j1,f2}$ 求偏导，可得：

$$ \begin{array}{l}
\frac{{\partial {\rm{\{ }}\frac{\lambda }{2}||V||_2^2 + \log (1 + exp( - {y_i}\phi (V,x))){\rm{\} }}}}{{\partial {V_{j1,f2}}}}\\
= \lambda \cdot {V_{j1,f2}} + \frac{{\partial \log (1 + exp( - {y_i}\phi (V,x)))}}{{\partial {V_{j1,f2}}}}\\
= \lambda \cdot {V_{j1,f2}} + \frac{{\partial \log (1 + exp( - {y_i}\phi (V,x)))}}{{\partial \phi }} \cdot \frac{{\partial \phi }}{{{V_{j1,f2}}}}\\
= \lambda \cdot {V_{j1,f2}} + \frac{{ - y}}{{1 + \exp (y\phi (V,x))}} \cdot {V_{j2,f1}}
\end{array} \tag{24} $$

1.4.4 时间复杂度

对于计算时间复杂度，由于式(18)无法做类似于式（10）的简化，因此FFM的计算时间复杂度为$O(kn^2)$。

对于训练时间复杂度，由于训练时，需要先根据式（18）计算$\phi$，复杂度为$O(kn^2)$，计算得到$\phi$后，还需要按照式（22）计算1次，按照式（21）计算$2k$次，按照式（23）计算$2k$次，按照式（24）计算$2k$次，也就是说，总的训练时间复杂度为：

$$O(kn^2) + 1 + 2k + 2k + 2k = O(kn^2) $$

因此，训练时间复杂度为$O(kn^2)$。

1.4.5 模型优化

特征归一化、样本归一化。

2. Recurrent Entity Network原理介绍

Recurrent Entity Network简称EntNet，最初在论文TRACKING THE WORLD STATE WITH RECURRENT ENTITY NETWORKS中提出，文中给出了lua+torch的代码地址。作者包括Facebook AI研究院的Mikael Henaff， Jason Weston(MemNN和MemN2N的作者)以及Yann LeCun.

Entity Network模型共分为Input Encoder、Dynamic Memory和Output Model三个部分。如下图的架构图所示：

EntNet使用了动态长期记忆，因此可以用在语言理解任务，QA等;
各个memory cell是独立的，因此EntNet可以看做是一系列共享权值的gated RNN。

输入为：

$$ {s_t} = \sum\limits_i {{f_i}}  \odot {e_i} $$

输入是一个固定长度的向量，用来表示一个sentence。$f_i$是需要学习的multiplicative mask, 使用这个mask的目的在于加入位置信息。 $e_i$是单词的embedding表示。

Dynamic memory为：

$$ \begin{array}{l}
{g_j} \leftarrow \sigma \left( {s_t^T{h_j} + s_t^T{w_j}} \right)\\
\widetilde {{h_j}} \leftarrow \phi \left( {U{h_j} + V{w_j} + W{s_t}} \right)\\
{h_j} \leftarrow {h_j} + {g_j} \odot \widetilde {{h_j}}\\
{h_j} \leftarrow \frac{{{h_j}}}{{\left\| {{h_j}} \right\|}}
\end{array} $$

输出为：

$$ \begin{array}{l}
{p_j} = soft\max \left( {{q^T}{h_j}} \right)\\
u = \sum\limits_j {{p_j}} {h_j}\\
y = R\phi \left( {q + Hu} \right)
\end{array} $$

3. FFM + Recurrent Entity Network

首先要将用于FFM的特征做处理，生成"feature index"和"feature value"，用于FFM做特征交叉。

feature_index是把所有特征进行了标序，feature1，feature2......featurem，分别对应0，1，2，3，...m，但是，请注意分类变量需要拆分！

就是说如果有性别：男|女|未知，三个选项。需要构造feature男，feature女，feature未知三个变量，而连续变量就不需要这样。

feature_value就是特征的值，连续变量按真实值填写，分类变量全部填写1。

更加形象的如下：

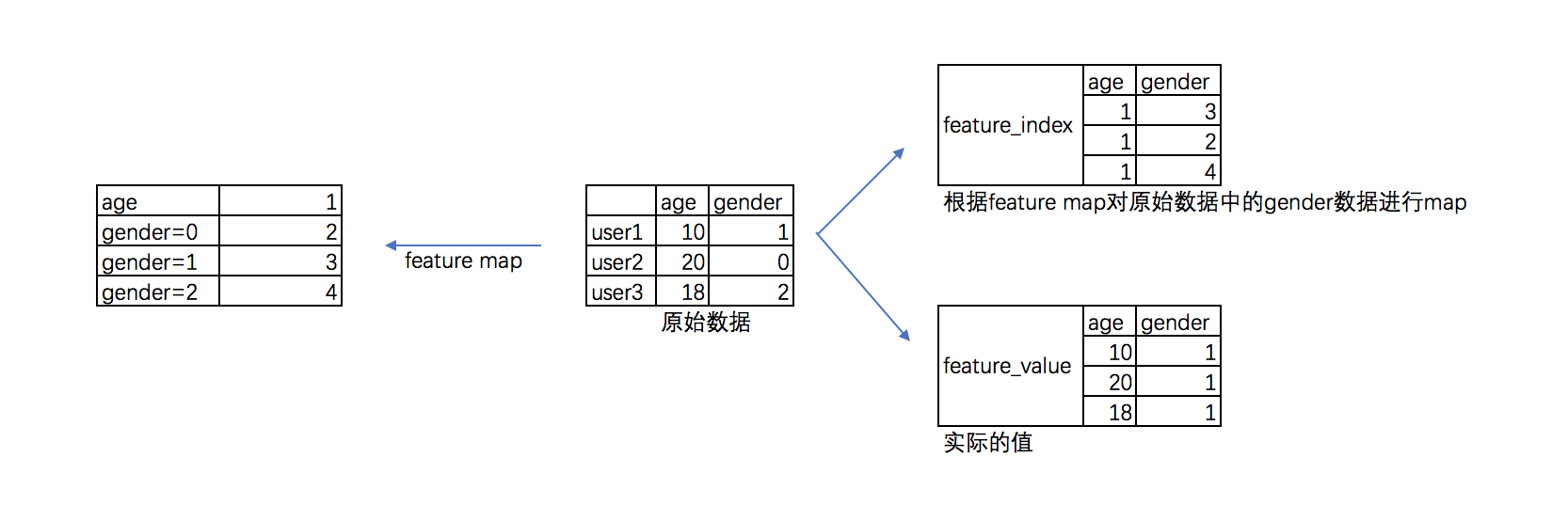
FFM模块代码实现如下（Tensorflow）：

    def ffm_module(self):
        # initial weights
        self.weights = dict()
        # feature_size * K
        self.weights["feature_embeddings"] = tf.Variable(
            tf.random_normal([self.feature_size, self.embedding_size], 0.0, 0.01), name="feature_embeddings")
        # feature_size * 1
        self.weights["feature_bias"] = tf.Variable(
            tf.random_uniform([self.feature_size, 1], 0.0, 1.0), name="feature_bias")
        input_size = self.field_size * self.embedding_size
        glorot = np.sqrt(2.0 / (input_size + 1))
        self.weights["use_fm_concat_weights"] = tf.Variable(
                        np.random.normal(loc=0, scale=glorot, size=(self.field_size+self.embedding_size, self.num_classes)),
                        dtype=np.float32)

        # model
        self.embeddings = tf.nn.embedding_lookup(self.weights["feature_embeddings"], self.feat_index)  # None * F * K
        feat_value = tf.reshape(self.feat_value, shape=[-1, self.field_size, 1])
        self.embeddings = tf.multiply(self.embeddings, feat_value)

        # ---------- first order term ----------
        self.y_first_order = tf.nn.embedding_lookup(self.weights["feature_bias"], self.feat_index)  # None * F * 1
        self.y_first_order = tf.reduce_sum(tf.multiply(self.y_first_order, feat_value), 2)  # None * F
        self.y_first_order = tf.nn.dropout(self.y_first_order, self.dropout_keep_fm[0])  # None * F

        # ---------- second order term ---------------
        # sum_square part
        self.summed_features_emb = tf.reduce_sum(self.embeddings, 1)  # None * K
        self.summed_features_emb_square = tf.square(self.summed_features_emb)  # None * K

        # square_sum part
        self.squared_features_emb = tf.square(self.embeddings)
        self.squared_sum_features_emb = tf.reduce_sum(self.squared_features_emb, 1)  # None * K

        # second order
        self.y_second_order = 0.5 * tf.subtract(self.summed_features_emb_square,
                                                self.squared_sum_features_emb)  # None * K
        self.y_second_order = tf.nn.dropout(self.y_second_order, self.dropout_keep_fm[1])  # None * K

        self.ffm_y = tf.concat([self.y_first_order, self.y_second_order], axis=1)
        self.ffm_y = tf.reshape(self.ffm_y, shape=[self.batch_size, self.field_size+self.embedding_size])
        self.ffm_y = tf.nn.dropout(self.activation(self.ffm_y), self.dropout_keep_fm[2])
        self.ffm_y = tf.matmul(self.ffm_y, self.weights["use_fm_concat_weights"])

EntityNet的核心代码：

    def rnn_story(self):
        """
        run rnn for story to get last hidden state
        input is:  story:                 [batch_size,story_length,embed_size]
        :return:   last hidden state.     [batch_size,embed_size]
        """
        # 1.split input to get lists.
        input_split=tf.split(self.story_embedding,self.story_length,axis=1) #a list.length is:story_length.each element is:[batch_size,1,embed_size]
        input_list=[tf.squeeze(x,axis=1) for x in input_split]           #a list.length is:story_length.each element is:[batch_size,embed_size]
        # 2.init keys(w_all) and values(h_all) of memory
        h_all=tf.get_variable("hidden_states",shape=[self.block_size,self.dimension],initializer=self.initializer)# [block_size,hidden_size]
        w_all=tf.get_variable("keys",          shape=[self.block_size,self.dimension],initializer=self.initializer)# [block_size,hidden_size]
        # 3.expand keys and values to prepare operation of rnn
        w_all_expand=tf.tile(tf.expand_dims(w_all,axis=0),[self.batch_size,1,1]) #[batch_size,block_size,hidden_size]
        h_all_expand=tf.tile(tf.expand_dims(h_all,axis=0),[self.batch_size,1,1]) #[batch_size,block_size,hidden_size]
        # 4. run rnn using input with cell.
        for i,input in enumerate(input_list):
            h_all_expand=self.cell(input,h_all_expand,w_all_expand,i) #w_all:[batch_size,block_size,hidden_size]; h_all:[batch_size,block_size,hidden_size]
        return h_all_expand #[batch_size,block_size,hidden_size]

    def cell(self,s_t,h_all,w_all,i):
        """
        parallel implementation of single time step for compute of input with memory
        :param s_t:   [batch_size,hidden_size].vector representation of current input(is a sentence).notice:hidden_size=embedding_size
        :param w_all: [batch_size,block_size,hidden_size]
        :param h_all: [batch_size,block_size,hidden_size]
        :return: new hidden state: [batch_size,block_size,hidden_size]
        """
        # 1.gate
        s_t_expand=tf.expand_dims(s_t, axis=1)       #[batch_size,1,hidden_size]
        g=tf.nn.sigmoid(tf.multiply(s_t_expand,h_all)+tf.multiply(s_t_expand,w_all))#shape:[batch_size,block_size,hidden_size]

        # 2.candidate hidden state
        #below' shape:[batch_size*block_size,hidden_size]
        h_candidate_part1=tf.matmul(tf.reshape(h_all,shape=(-1,self.dimension)), self.U) + tf.matmul(tf.reshape(w_all,shape=(-1,self.dimension)), self.V)+self.h_bias
        # print("======>h_candidate_part1:",h_candidate_part1) #(160, 100)
        h_candidate_part1=tf.reshape(h_candidate_part1,shape=(self.batch_size,self.block_size,self.dimension)) #[batch_size,block_size,hidden_size]
        h_candidate_part2=tf.expand_dims(tf.matmul(s_t,self.W)+self.h2_bias,axis=1)              #shape:[batch_size,1,hidden_size]
        h_candidate=self.activation(h_candidate_part1+h_candidate_part2,scope="h_candidate"+str(i))   #shape:[batch_size,block_size,hidden_size]

        # 3.update hidden state
        h_all=h_all+tf.multiply(g,h_candidate) #shape:[batch_size,block_size,hidden_size]

        # 4.normalized hidden state
        h_all=tf.nn.l2_normalize(h_all,-1) #shape:[batch_size,block_size,hidden_size]
        return h_all  #shape:[batch_size,block_size,hidden_size]

将两者结合起来：

    def output_module(self):
        """
        1.use attention mechanism between query and hidden states, to get weighted sum of hidden state. 2.non-linearity of query and hidden state to get label.
        input: query_embedding:[batch_size,embed_size], hidden state:[batch_size,block_size,hidden_size] of memory
        :return:y: predicted label.[]
        """
        # 1.use attention mechanism between query and hidden states, to get weighted sum of hidden state.
        # 1.1 get possibility distribution (of similiarity)
        p = tf.nn.softmax(tf.multiply(tf.expand_dims(self.query_embedding, axis=1), self.hidden_state)) #shape:[batch_size,block_size,hidden_size]<---query_embedding_expand:[batch_size,1,hidden_size]; hidden_state:[batch_size,block_size,hidden_size]
        # 1.2 get weighted sum of hidden state
        u = tf.reduce_sum(tf.multiply(p, self.hidden_state), axis=1)  # shape:[batch_size,hidden_size]<----------([batch_size,block_size,hidden_size],[batch_size,block_size,hidden_size])

        # 2.non-linearity of query and hidden state to get label
        H_u_matmul = tf.matmul(u, self.H) + self.h_u_bias  # shape:[batch_size,hidden_size]<----([batch_size,hidden_size],[hidden_size,hidden_size])

        activation = self.activation(self.query_embedding + H_u_matmul, scope="query_add_hidden")           #shape:[batch_size,hidden_size]
        activation = tf.nn.dropout(activation, keep_prob=self.dropout_keep_prob) #shape:[batch_size,hidden_size]
        y = tf.matmul(activation, self.R) + self.y_bias  # shape:[batch_size,vocab_size]<-----([batch_size,hidden_size],[hidden_size,vocab_size])

        # FFM layer
        if self.use_fm:
            self.ffm_module()
            y = tf.add(y, self.ffm_y)
        return y  # shape:[batch_size,vocab_size]

详细demo参考：playground_ffm_entitynet.zip。

参考文章：

1. https://www.jianshu.com/p/71d819005fed

2. https://blog.csdn.net/Irving_zhang/article/details/79204426

3. https://blog.csdn.net/jediael_lu/article/details/77772565