HDU - 5513 Efficient Tree(轮廓线DP)

前言

• 最近学了基于连通性的状压DP，也就是插头DP，写了几道题，发现这DP实质上就是状压+分类讨论，轮廓线什么的也特别的神奇。下面这题把我WA到死…

---

HDU-5531 Efficient Tree

• 给出一个n∗mn*mn∗m的网格图，以及相邻四联通格子之间的边权。
  
  对于命题xxx，如果xxx成立，那么 [x]=1[x]=1[x]=1，否则 [x]=0[x]=0[x]=0
  
  对于一颗生成树，每个点的贡献为 1+[有一条连向上的边]+[有一条连向左的边]1+[有一条连向上的边]+[有一条连向左的边]1+[有一条连向上的边]+[有一条连向左的边]。这棵树的贡献为所有点的贡献之积。要求：

  • 最小生成树的边权和
  • 所有最小生成树的贡献之和。

  n&lt;=800,m&lt;=7n&lt;=800, m&lt;=7n<=800,m<=7

• 由于mmm最大只有777，考虑轮廓线DP：

  • f(i,j,S)f(i,j,S)f(i,j,S) 表示当前在 (i,j)(i,j)(i,j)这个点，轮廓线上方的格子联通情况为SSS的边权之和
  • g(i,j,S)g(i,j,S)g(i,j,S) 表示当前在 (i,j)(i,j)(i,j)这个点，轮廓线上方的格子联通情况为SSS的贡献之和
    
    
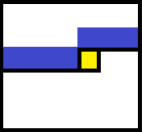
  • 黄色格子就是当前考虑的点，蓝色部分就是上一次状压的 mmm 个格子
  • 此处的SSS是用最小表示法状压的，状态是长度为 mmm 的 888 进制数，每个位置上的值表示每一个蓝色格子在哪一个联通块里
  • 这里的状压与普通插头DP有点不同，普通插头DP的状态长度是m+1m+1m+1，因为多算上了中间那一条竖着的轮廓线，而这里并不用。

• 转移比较简单，只要注意两点：

  • 如果当前格子上面的格子在单独一个联通块，那么这条向上的边必须选，否则就无法形成一棵联通的树。
  • 如果上面的格子和左边的格子在同一个联通块就不能合并，否则构成了一个环。

AC代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 805, MAXM = 10;
const int HASH = 10007, NUM = 1000005;
const int mod = 1e9+7, inf = 0x3f3f3f3f;
struct node {
    int w, sum;
    node(int _w=0, int _sum=0):w(_w), sum(_sum){}
    inline node operator +(const node &t)const {
        if(w < t.w) return *this;
        if(w > t.w) return t;
        return node(w, (sum+t.sum)%mod);
    }
    inline node operator +(const int &t)const {
        return node(w+t, sum);
    }
    inline node operator *(const int &t)const {
        return node(w, 1ll*sum*t%mod);
    }
};
int n, m;
int L[MAXN][MAXM], U[MAXN][MAXM];
struct HashMap {
    int val[NUM], adj[HASH], pre[NUM], tot;
    node f[NUM];
    inline void init() {
        memset(adj, -1, sizeof adj); tot = 0;
    }
    inline void insert(const int &x, const node &tmp) {
        int u = x % HASH;
        for(int i = adj[u]; ~i; i = pre[i])
            if(val[i] == x) {
                f[i] = f[i] + tmp; return;
            }
        val[++tot] = x; pre[tot] = adj[u]; adj[u] = tot; f[tot] = tmp;
    }
}h[2];
int msk[MAXM], id[MAXM];
inline void decode(int x) {
    for(int i = m; i; --i, x>>=3) msk[i] = x&7;
}
inline int encode(const int &m) {
    int res = 0, cur = 0;
    memset(id, -1, sizeof id);
    id[0] = 0;
    for(int i = 1; i <= m; ++i) {
        if(id[msk[i]] == -1) id[msk[i]] = ++cur;
        res = (res<<3)|id[msk[i]];
        //注意这里不能 msk[i]=id[msk[i]], 否则改变了 msk[i]的值, dp函数中的x,y值就不对了
    }
    return res;
}
inline void dp(const int &i, const int &j, const int &now) {
    for(int k = 1; k <= h[now^1].tot; ++k) {
        decode(h[now^1].val[k]);
        int x = msk[j-1], y = msk[j];
        bool one = 1;
        for(int l = 0; l <= m; ++l) //看是否是独立的联通块
        	if(l != j && msk[l] == y) { one = 0; break; }
        if(!one) { //自成联通块
            msk[j] = 8; //赋值为不可能出现的8
            h[now].insert(encode(m), h[now^1].f[k]);
            msk[j] = y;
        }
        if(i > 1)
        	h[now].insert(encode(m), (h[now^1].f[k] + U[i][j])*2);//只连左边
        if(j > 1 && !one) {
            msk[j] = x;
            h[now].insert(encode(m), (h[now^1].f[k] + L[i][j])*2);//只连上边
            msk[j] = y;
        }
        if(i > 1 && j > 1 && x != y) { //两边都连
            for(int l = 0; l <= m; ++l) if(msk[l] == x) msk[l] = y;
            h[now].insert(encode(m), (h[now^1].f[k] + L[i][j] + U[i][j])*3);
        }
    }
}
int main () {
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; ++kase) {
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; ++i)
            for(int j = 2; j <= m; ++j)
                scanf("%d", &L[i][j]);
        for(int i = 2; i <= n; ++i)
            for(int j = 1; j <= m; ++j)
                scanf("%d", &U[i][j]);
        int now = 0; h[now].init(); h[now].insert(0, node(0, 1));
        for(int i = 1; i <= n; ++i)
            for(int j = 1; j <= m; ++j) {
				now ^= 1; h[now].init();
                dp(i, j, now);
            }
        node ans = node(inf, 0);
        for(int i = 1; i <= h[now].tot; ++i) {
            bool flag = 1;
            decode(h[now].val[i]);
            for(int j = 1; j < m; ++j)
                if(msk[j] != msk[j+1]) { flag = 0; break; }
            if(flag) ans = ans + h[now].f[i];
        }
        printf("Case #%d: %d %d\n", kase, ans.w, ans.sum);
    }
}

PS：PS：PS：

• 我之所以WA就是因为encodeencodeencode函数里改变了mskmskmsk的值，出来后dpdpdp函数里的x,yx,yx,y就不对了，WA到自闭…

• 还有我的代码只用了msk[1...m]msk[1...m]msk[1...m]，第000位没用