20180429模拟赛T1——添边问题

【问题描述】

没有环的有向图称为有向无环图，这是一个多么美好的结构吖。

如果有一张有 N 个点的有向图，我们可能需要删掉一些边使它变成一张有向无环图。假设初始时我们只有 N 个互不相连的点，当然它也是一张有向无环图。依次给出 T 条边和每条边的方向。 每给出一条边就要立即决定是否要加入这一条边，使得这张图始终是一张有向无环图(意思是：按顺序处理每条边，能加就加，让你模拟这个过程，自环不能加入)。计算在满足要求的情况下一共有多少条边没有被加入。如果所有边都可以加入这张图则输出 0。

【输入格式】

第一行为两个整数：N(1<=N<=250)，T(0<=T<=100,000)。接下来 T 行，每行两个整数 x,y(1 <=x,y<= N)，表示一条从 x 到 y 的单向边。

【输出格式】

一个整数，表示没有被加入的边数。

【样例输入】

3 6

1 2

1 3

3 1

2 1

1 2

2 3

【样例输出】

2

【样例说明】

1-->2，之前 2-->1 没有路径，不会造成环，加入

1-->3，之前 3-->1 没有路径，不会造成环，加入

3-->1，之前 1-->3 有路径，使得图有环，不加入

2-->1，之前 1-->2 有路径，不加入

1-->2 , 之前 2-->1 没有路径，加入

2-->3，之前 3-->2 没有路径，加入

因此答案是 2

【数据规模】

对于40%的数据，n<=50,T<=1000

对于90%的数据，n<=150,T<=100000

对于100%的数据，n<=250,T<=100000

题解

我们用\(f[i][j]\)表示\(i\)是否能到\(j\)(1:能 0:不能)。首先忽略重边。判断一条边能否加入显然是\(O(1)\)的，只要看看\(f[y][x]\)是不是\(1\)即可。

若加入，就要维护连通性。

如图，对于两个点\(A,B\)，圈表示点集，箭头表示边，连边\(A\to B\)后我们又要连蓝边与绿边。

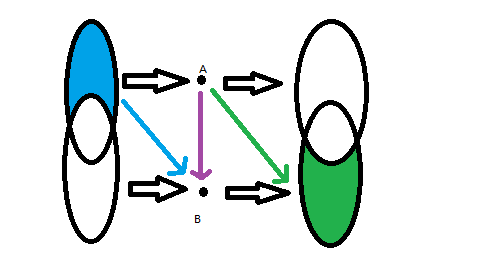
不难发现，我们可以把\(A\)与蓝色集合、\(B\)与绿色集合合并，于是问题就变成了：

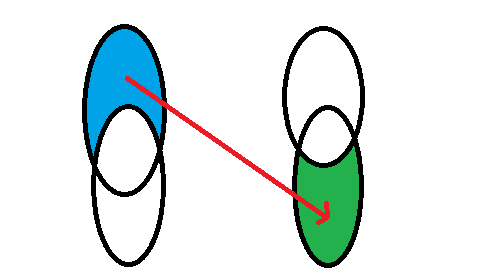
蓝色集合向绿色集合连边。

蓝色集合为能到达\(A\)的点集；绿色集合表示能到达\(B\)的点集。

\(n^2\)大力连边即可。

我的代码

#include <cstring>
#include <fstream>

using namespace std;

ifstream fin("stock.in");
ofstream fout("stock.out");

const int maxm=100000;
const int maxn=256;

int a[maxn][maxn];
int b[maxm],c[maxm];

int main()
{
	int n, m;
	fin >> n >> m;
	int ans=0;
	for(int i=0; i<m; ++i)
	{
		int aa, bb;
		fin >> aa >> bb;
		if(aa==bb || a[bb][aa]) ans++;
		else
		{
			int k1=0;
			int k2=0;
			b[++k1]=aa;
			c[++k2]=bb;
			for(int j=1; j<=n; ++j)
				if(a[j][aa] && !a[j][bb])
					b[++k1]=j;
			for(int j=1; j<=n; ++j)
				if(a[bb][j] && !a[aa][j])
					c[++k2]=j;
			for(int j=1; j<=k1; ++j)
				for(int k=1; k<=k2; ++k)
					a[b[j]][c[k]]=1;
		}
	}
	fout << ans << '\n';
	return 0;
}

bitset优化

以上代码是可过的，但还可以用bitset优化一下，上一发zd大佬的代码。

#include <iostream>
#include <bitset>
#include <cstdio>

using namespace std;

typedef int ll;

inline char gc()
{
	static char buf[1<<14],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<14,stdin),p1==p2)?EOF:*p1++;
}

#define dd c=gc()
inline ll read()
{
	ll x=0,f=1;
	char dd;
	for(; !isdigit(c); dd)if(c=='-')f=-1;
	for(; isdigit(c); dd)x=(x<<1)+(x<<3)+(c^48);
	return x*f;
}
#undef dd

inline void write(ll x)
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10|48);
}

bitset<252>a[252];

int main()
{
	freopen("stock.in","r",stdin);
	freopen("stock.out","w",stdout);
	register ll n=read(),ans=0;
	for (register ll i=0; i<n; ++i) a[i][i]=1;
	for (register ll m=read(),x,y; m; --m)
	{
		x=read()-1,y=read()-1;
		if (a[y][x]) ++ans;
		else if (!a[x][y])
			for (register ll i=0; i<n; ++i)
			{
				if (a[i][x]) a[i]=a[i]|a[y];
			}
	}
	return write(ans),0;
}