【HDU1730】Northcott Game（Nim问题）

Northcott Game

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3101    Accepted Submission(s): 1355

Problem Description

　　Tom和Jerry正在玩一种Northcott游戏，可是Tom老是输，因此他怀疑这个游戏是不是有某种必胜策略，郁闷的Tom现在向你求救了，你能帮帮他么？
游戏规则是这样的：
　　如图所示，游戏在一个n行m列（1 ≤ n ≤ 1000且2 ≤ m ≤ 100）的棋盘上进行，每行有一个黑子（黑方）和一个白子（白方）。执黑的一方先行，每次玩家可以移动己方的任何一枚棋子到同一行的任何一个空格上，当然这过程中不许越过该行的敌方棋子。双方轮流移动，直到某一方无法行动为止，移动最后一步的玩家获胜。Tom总是先下（黑方）。图1是某个初始局面，图二是Tom移动一个棋子后的局面（第一行的黑子左移两步）。

图1

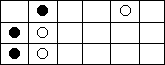
图2

 

Input

　　输入数据有多组。每组数据第一行为两个整数n和m，由空格分开。接下来有n行，每行两个数Ti，Ji (1 ≤ Ti, Ji ≤ m)分别表示Tom和Jerry在该行棋子所处的列数。
　　注意：各组测试数据之间有不定数量的空行。你必须处理到文件末。

 

Output

对于每组测试数据输出一行你的结果。如果当前局面下Tom有必胜策略则输出“I WIN!”，否则输出“BAD LUCK!”。

 

Sample Input

3 6
4 5
1 2
1 2

3 6
4 5
1 3
1 2

 

Sample Output

BAD LUCK!
I WIN!

 

这道题是典型的博弈论Nim问题 我们先了解一下Nim问题

理论铺垫。。。。

1、定义P-position和N-position：其中P代表Previous，N代表Next。直观的说，上一次move的人有必胜策略的局面是P-position，也就是“先手必败”，现在轮到move的人有必胜策略的局面是N-position，也就是“先手可保证必胜”。

（1）.无法进行任何移动的局面（也就是terminal position）是P-position；

（2）.可以移动到P-position的局面是N-position；

（3）.所有移动都导致N-position的局面是P-position。

2、P/N状态有如下性质：

（1）、若面临末状态者为获胜则末状态为胜态否则末状态为必败态。
（2）、一个局面是胜态的充要条件是该局面进行某种决策后会成为必败态。
（3）、一个局面是必败态的充要条件是该局面无论进行何种决策均会成为胜态

3、P点： 即必败点，某玩家位于此点，只要对方无失误，则必败；

N点： 即必胜点，某玩家位于此点，只要自己无失误，则必胜。

4、取石子游戏算法实现

步骤1:将所有终结位置标记为必败点（P点）；

步骤2: 将所有一步操作能进入必败点（P点）的位置标记为必胜点（N点）

步骤3:如果从某个点开始的所有一步操作都只能进入必胜点（N点） ，则将该点标记为必败点（P点） ；

步骤4: 如果在步骤3未能找到新的必败（P点），则算法终止；否则，返回到步骤2

1、问题模型：有三堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

2、解决思路：用（a，b，c）表示某种局势，显证（0，0，0）是第一种奇异局势，无论谁面对奇异局势，都必然失败。第二种奇异局势是（0，n，n），只要与对手拿走一样多的物品，最后都将导致（0，0，0）。

搞定这个问题需要把必败态的规律找出：(a,b,c)是必败态等价于a^b^c=0(^表示异或运算）。

证明:(1)任何p(a,b,c)=0的局面出发的任意局面(a,b,c’);一定有p(a,b,c’)不等于0。否则可以得到c=c’。

（2）任何p(a,b,c)不等于0的局面都可以走向 p(a,b,c)=0的局面

(3）对于 (4,9,13) 这个容易验证是奇异局势

其中有两个8，两个4，两个1，非零项成对出现，这就是尼姆和为
 零的本质。别人要是拿掉13里的8或者1，那你就拿掉对应的9  中的那个8或者1；别人要是拿        掉13里的4，你就拿掉4里的4；  别人如果拿掉13里的3，就把10作分解，然后想办法满
足非零项成对即可。

3、推广一：如果我们面对的是一个非奇异局势（a，b，c），要如何变为奇异局势呢？假设 a < b< c,我们只要将 c 变为 a^b,即可,因为有如下的运算结果: a^b^(a^b)=(a^a)^(b^b)=0^0=0。要将c 变为a^b，只从 c中减去 c-（a^b）

4、推广二：当石子堆数为n堆时，则推广为当对每堆的数目进行亦或之后值为零是必败态。

再回到这道题 我们只需要把每行之间的空格数相互异或最后求得结果判断是不是0就可以了。。

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <cstdlib>
 using namespace std;
 
 int main(){
     int n, m;
     while(scanf("%d%d", &n, &m)!=EOF){
         m = ;                          //这里注意m并没有什么用处我就懒得多定义一个变量了直接拿来用了
         int a, b;
 
         while(n--){
             scanf("%d%d", &a, &b);
             m ^= abs(a-b) - ;
         }
 
         if(m){
             printf("I WIN!\n");
         }
         else{
             printf("BAD LUCK!\n");
         }
     }
     return ;
 }

Alpha