[Luogu P3953] 逛公园 (最短路+拓扑排序+DP)

题面

传送门：https://www.luogu.org/problemnew/show/P3953

---

Solution

这是一道神题

首先，我们不妨想一下K=0，即求最短路方案数的部分分。

我们很容易可以想到一个做法，就是魔改迪杰斯特拉做法：

如果一个点可以更新到达其他点的距离，那个点的方案数就是这个点的方案数；如果一个点所更新出来的距离和之前的相等，那个点的方案数加等当前点的方案数。

用式子可以表现为：

f[j]=f[i] (dis[j]>dis[i]+x)  

f[j]+=f[i] (dis[j]==dis[i]+x)

(i表示当前点，j表示它更新的点，x为i到j那条路的距离)

那我们怎么保证它的顺序不会出错，即如何保证一个点去更新其他点的方案数的时候，这个点的方案数是正确的呢？

事实上，这种做法就是一种DP。

那么，对于K！=0的情况怎么处理呢？

观察数据，我们会发现K最大只有50。

因此，我们可以考虑在DP上加一维来解决这个K值。

考虑这样设状态：

f[i][j] 表示到达i点，距离为dis[i]+j 的方案数

转移非常好写

f[i][j] = sigema (f[k][dis[i]+j-dis[k]-a]) (k为直接连到i的点，a表示它们之间的边权)

初始化其实我们在30分做法中就已经求好了。

转移顺序是个问题。

我们显然可以在外层枚举j，问题是，有时候，dis[i]+j-dis[k]-a会等于j，如果枚举i的顺序错了，答案肯定会跟着错。

对于dis[i]+j-dis[k]-a==j 的点，肯定是k去更新i，又因为边权没有负值，所以我们就可以按照dis从小到大去去枚举i的值。

以上是没有零边的做法。

对于有零边的情况，我们刚刚的做法就会出问题。如图：

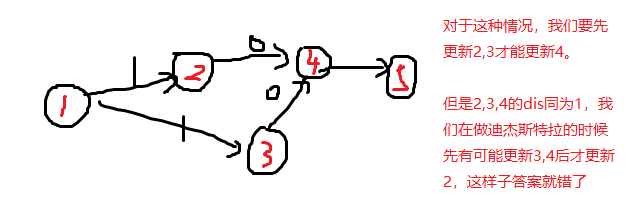
所以说，我们把原图转换一下，只保留0边，对新图做拓扑排序。

如果做完拓扑排序之后，有几个点没有进入过排序中，就说明这个图有零环，就gg了。

我们把拓扑序做完之后再执行原来有的最短路和dp，这样就不会错了。

就酱，我们就嘴巴AC这道题啦o(*￣▽￣*)o 。

事实上，这样做并A不了，因为这题TM卡常(╯°Д°)╯︵┻━┻

然后，你会被卡30分并因此退役（或者是开O2A掉这道题（但是NOIP中并不开O2，所以你还是因此退役了））

---

Code

//Luogu P3953 逛公园
//Sep,18th,2018
//最短路+拓扑排序+DP+卡常神题
// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=100000+100;
const int M=50+5;
const int inf=0x3f3f3f3f;
struct DIS
{
    int dis,no,zero;
}dis[N];
bool cmp(DIS A,DIS B)
{
    if(A.dis==B.dis)
        return A.zero<B.zero;
    return A.dis<B.dis;
}
struct road
{
    int to,w;
    road(int A,int B)
    {
        to=A,w=B;
    }
    friend bool operator < (road A,road B)
    {
        if(A.w==B.w)
            return dis[A.to].zero > dis[B.to].zero;
        return A.w > B.w;
    }
};
vector <road> e[N],rev[N];
int n,m,K,poi,T,rd[N],dl2[N],front2,tail2,dis2[N];
long long f[N][M];
priority_queue <road,vector<road> > dl;
bool vis[N];
void dj()
{
    for(int i=1;i<=n;i++)
        dis[i].dis=inf,dis[i].no=i;
    dis[1].dis=0;
    memset(dis2,0x3f,sizeof dis2);
    dis2[1]=0;
    while(dl.empty()==false) dl.pop();
    memset(vis,0,sizeof vis);
    dl.push(road(1,0));
    f[1][0]=1;
    int cnt=0;
    while(cnt!=n and dl.empty()==false)
    {
        road temp=dl.top();
        dl.pop();
        if(vis[temp.to]==true) continue;
        vis[temp.to]=true;
        int now=temp.to,dis_now=temp.w;
        for(int i=0;i<int(e[now].size());i++)
            if(dis_now+e[now][i].w < dis[e[now][i].to].dis)
            {
                f[e[now][i].to][0]=f[now][0];
                dis[e[now][i].to].dis=dis_now+e[now][i].w;
                dis2[e[now][i].to]=dis_now+e[now][i].w;
                dl.push(road(e[now][i].to,dis[e[now][i].to].dis));
            }
            else if(dis_now+e[now][i].w == dis[e[now][i].to].dis)
                f[e[now][i].to][0]=(f[e[now][i].to][0]+f[now][0])%poi;
    }
}
void GetTP()
{
    tail2=front2=0;
    memset(vis,0,sizeof vis);
    for(int i=1;i<=n;i++)
        if(rd[i]==0)
            dl2[tail2++]=i;
    int cnt=0;
    while(tail2>front2)
    {
        dis[dl2[front2]].zero=++cnt;
        vis[dl2[front2]]=true;
        for(int i=0;i<int(e[dl2[front2]].size());i++)
            if(e[dl2[front2]][i].w==0 and vis[e[dl2[front2]][i].to]==false)
            {
                rd[e[dl2[front2]][i].to]--;
                if(rd[e[dl2[front2]][i].to]==0)
                    dl2[tail2++]=e[dl2[front2]][i].to;
            }
        front2++;
    }
}
int main()
{
    T=read();
    for(int i=1;i<N;i++)
        e[i].reserve(4),rev[i].reserve(4);
    for(;T>0;T--)
    {
        memset(f,0,sizeof f);
        memset(rd,0,sizeof rd);
        n=read(),m=read(),K=read(),poi=read();
        for(int i=1;i<=n;i++)
            e[i].clear(),rev[i].clear();
        for(int i=1;i<=m;i++)
        {
            int a=read(),b=read(),c=read();
            e[a].push_back(road(b,c));
            rev[b].push_back(road(a,c));
            if(c==0)
                rd[b]++;
        }

        GetTP();
        bool OK=true;
        for(int i=1;i<=n;i++)
            if(vis[i]==false)
                OK=false;
        if(OK==false)
        {
            printf("-1\n");
            continue;
        }
        dj();

        sort(dis+1,dis+1+n,cmp);
        for(int j=1;j<=K;j++)
            for(int i=1;i<=n;i++)
                for(int k=0;k<int(rev[dis[i].no].size());k++)
                {
                    int t=dis[i].no,s=rev[t][k].to;
                    if(dis2[t]!=inf and dis2[s]!=inf and dis2[t]+j-dis2[s]-rev[t][k].w>=0 )
                        f[t][j]=(f[t][j]+f[s][dis2[t]+j-dis2[s]-rev[t][k].w])%poi;
                }

        long long ans=0;
        for(int i=0;i<=K;i++)
            ans=(ans+f[n][i])%poi;
        printf("%lld\n",ans);
    }
    return 0;
}