读Twinsen的深入探索透视投影变换

2017.10.16更新，分割线下面是以前的文字，有表达的意思，却言不达意，实属羞耻，看官只需看前面文字即可。

Twinsen大神的《深入探索透视投影变换》有几个点说得不够清晰，我这里提一下：

1.p'代表的是近平面的投影点，P'代表的是p'映射到单位立方体后的投影点；

2.原文：事实上是透视投影变换由两步组成：

　　1）  用透视变换矩阵把顶点从视锥体中变换到裁剪空间的CVV中。

　　2）  CVV裁剪完成后进行透视除法（一会进行解释）。

故，该文求的是第1）步的那个变换矩阵，只不过用到了第2步的信息来约束，因为这些约束很有用（单位立方体），所以该文先求得透视除法后的坐标点P'，然后返回来*w求得变换矩阵。这也是该文大量篇幅所做的：在2）的约束下求P'。

3.那P'*w和p'什么关系？即p'和1）中那个变换矩阵什么关系？看下图：

　　　　视空间=》p'=》单位立方体空间

　　　　视空间=》裁剪空间=》单位立方体空间

　　P'*w就是裁剪空间的坐标，而p'不是，但因为他们都处于中间流程，所以容易混淆！事实上，p'不过是求单位立方空间坐标的过渡。

　　注：顶点shader输入是模型空间坐标，输出是裁剪空间坐标！

4.以上3点很重要，也是原文没注意到却影响阅读效果的细节，那问题来了，为什么要分1）2）步，不直接拿P'给后续流水线？其他的俺不知，但显然P'如下格式是不易构造变换矩阵的:

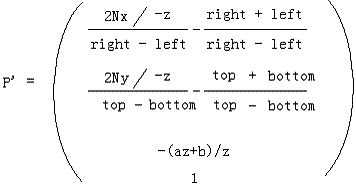
=======================羞耻分割线=======================

首先感谢Twinsen大神在此块的知识分享，我在好几篇文章中解惑不少，这篇文章是针对《深入探索透视投影变换》的个人看法，本来是打算直接评论中交流，但为了方便自己复习就写了篇随笔记一下，本文是基本copy原文中间那部分，只是进行了一点小改动，红色字体标出。

原文地址：http://blog.csdn.net/popy007/article/details/1797121

透视投影变换

好，有了上面两个理论知识，我们开始分析这次的主角——透视投影变换。这里我们选择OpenGL的透视投影变换进行分析，其他的APIs会存在一些差异，但主体思想是相似的，可以类似地推导。经过相机矩阵的变换，顶点被变换到了相机空间。这个时候的多边形也许会被视锥体裁剪，但在这个不规则的体中进行裁剪并非那么容易的事情，所以经过图形学前辈们的精心分析，裁剪被安排到规则观察体(Canonical View Volume, CVV)中进行，CVV是一个正方体，x, y, z的范围都是[-1，1]，多边形裁剪就是用这个规则体完成的。所以，事实上是透视投影变换由两步组成：

1）  用透视变换矩阵把顶点从视锥体中变换到裁剪空间的CVV中。

2）  CVV裁剪完成后进行透视除法（一会进行解释）。

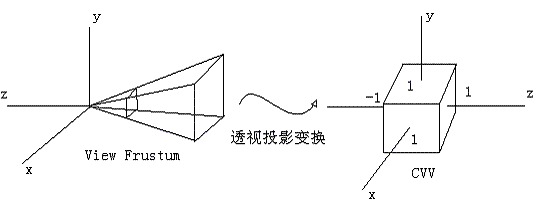
我们一步一步来，我们先从一个方向考察投影关系。

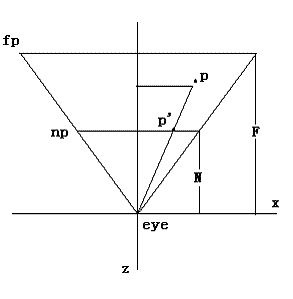
上图是右手坐标系中顶点在相机空间中的情形。设P(x,z)是经过相机变换之后的点，视锥体由eye——眼睛位置，np——近裁剪平面，fp——远裁剪平面组成。N是眼睛到近裁剪平面的距离，F是眼睛到远裁剪平面的距离。投影面可以选择任何平行于近裁剪平面的平面，这里我们选择近裁剪平面作为投影平面。设P’(x’,z’)是投影之后的点，则有z’ = -N。通过相似三角形性质，我们有关系：

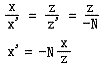
同理，有

这样，我们便得到了P投影后的点P’

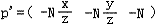
从上面可以看出，投影的结果z’始终等于-N，在投影面上。实际上，z’对于投影后的P’已经没有意义了，这个信息点已经没用了。但对于3D图形管线来说，为了便于进行后面的片元操作，例如z缓冲消隐算法，有必要把投影之前的z保存下来，方便后面使用。

假设p'完成透视除法后变成p'',由于各种原因（原文有说明），需要把p''的z'变量变成 -(az+b)/z，即

p' = (x', y', z') = (x', y', -(az+b)/z)

你一定会问为什么要把z'写成那样子

有三个原因：

0）后面投影之后的光栅化阶段，要通过x'和y'对z进行线性插值，以求出三角形内部片元的z，进行z缓冲深度测试。在数学上，投影后的x'和y'，与z不是线性关系，与1/z才是线性关系。而正是1/z的线性关系，即-a+b/z。用这个1/z的线性组合值和x'、y'进行插值才是正确的。（2013年11月补充条目。对此感到迷惑的读者可以参考《深入探索透视纹理映射》，里面从细节上说明了这个问题。）

1）  P’的3个代数分量统一地除以分母-z，易于使用齐次坐标变为普通坐标来完成，使得处理更加一致、高效。

2）  后面的CVV是一个x',y',z'的范围都为[-1，1]的规则体，便于进行多边形裁剪。而我们可以适当的选择系数a和b，使得这个式子在z = -N的时候值为-1，而在z = -F的时候值为1，从而在z方向上构建CVV。

接下来我们就求出a和b：

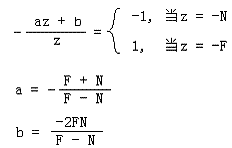
但这个时候我们只完成了z'统一到[-1,1]，x'和y'还没完成，这个也同理根据线性差值，由P'和P''得到：

对于P'，我们知道-Nx / z的有效范围是投影平面的左边界值（记为left）和右边界值（记为right），即[left, right]，-Ny / z则为[bottom, top]。而现在我们想把把P''的x'束缚在[-1,1]中，即-Nx / z属于[left, right]映射到[-1, 1]，-Ny / z属于[bottom, top]映射到y属于[-1, 1]中。你想到了什么？哈，就是我们简单的线性插值，你都已经掌握了！我们解决掉它：

【注，上面我用的是原文的图片，实际上，Nx的x是x，其他单独的x应该改成x'，y同理】

这样就可以得到P''=(x', y' ,z')了，我们前面说过的透视变换分2步，第一步是用透视矩阵变换，第二步是透视除法，我们得到的P''是透视除法的结果，而我们需要得到的是透视矩阵，所以必须“回退”一下，即P'''是透视矩阵变换的结果：

P''' = P'' * -z（-z才是正的），然后从P'''中拆解出透视矩阵即可P''' = M * (x, y, z,1)^T:

M就是最终的透视变换矩阵。相机空间中的顶点，如果在视锥体中，则变换后就在CVV中。如果在视锥体外，变换后就在CVV外。而CVV本身的规则性对于多边形的裁剪很有利。OpenGL在构建透视投影矩阵的时候就使用了M的形式。注意到M的最后一行不是(0 0 0 1)而是(0 0 -1 0)，因此可以看出透视变换不是一种仿射变换，它是非线性的。另外一点你可能已经想到，对于投影面来说，它的宽和高大多数情况下不同，即宽高比不为1，比如640/480。而CVV的宽高是相同的，即宽高比永远是1。这就造成了多边形的失真现象，比如一个投影面上的正方形在CVV的面上可能变成了一个长方形。解决这个问题的方法就是在对多变形进行透视变换、裁剪、透视除法之后，在归一化的设备坐标(Normalized Device Coordinates)上进行的视口(viewport)变换中进行校正，它会把归一化的顶点之间按照和投影面上相同的比例变换到视口中，从而解除透视投影变换带来的失真现象。进行校正前提就是要使投影平面的宽高比和视口的宽高比相同。

此外，原文中说CVV是一个正方体，x, y, z的范围都是[-1，1]，但推导过程中一直以透视除法后的坐标为[-1，1]为基准计算的，是不是透视除法后才得到CVV？

总结：本文认为原文这样的写法是错误的：，也因此导致了一些疑惑，记此文方便和Twinsen交流，如有误，麻烦指正。