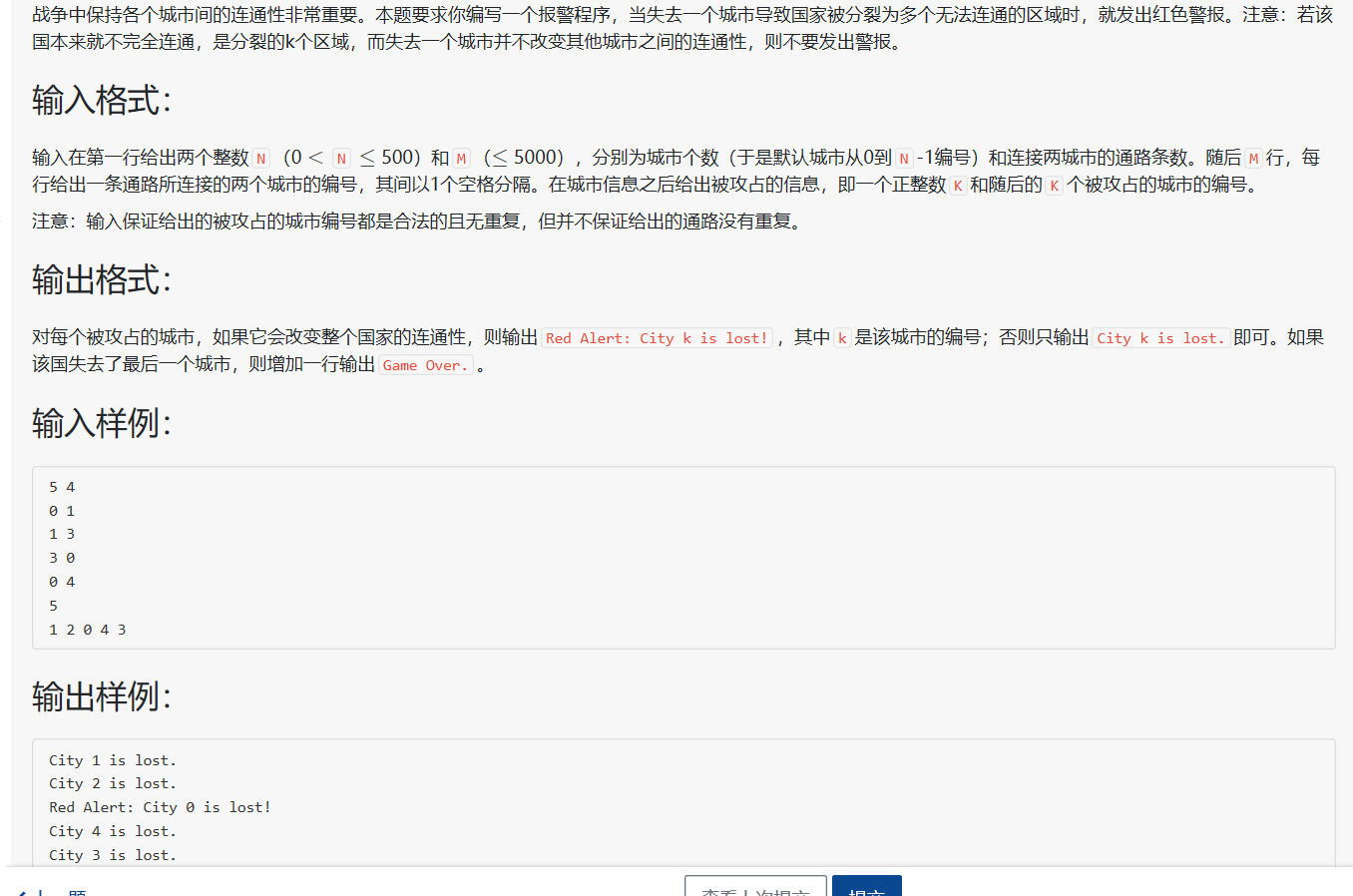
L2-013 红色警报 (25分) 并查集复杂度

代码：

  1 /*
  2 这道题也是简单并查集，并查集复杂度：
  3 空间复杂度为O(N)，建立一个集合的时间复杂度为O(1)，N次合并M查找的时间复杂度为O(M Alpha(N))，
  4 这里Alpha是Ackerman函数的某个反函数，在很大的范围内（人类目前观测到的宇宙范围估算有10的80次方个原子，
  5 这小于前面所说的范围）这个函数的值可以看成是不大于4的，所以并查集的操作可以看作是线性的。
  6
  7 不弄清楚一个算法的复杂度就是不敢很用
  8
  9
 10 题解：
 11 在询问时，标记当前结点，然后将其余的结点并查集一次，求出集合数，
 12 如果集合数相等或者前面完整结点的集合数+1=当前集合数，那么也就说明了去掉当前结点是没什么影响的，
 13 其余情况就是有影响
 14
 15 思路很好想，了解了复杂度之后就敢下手了
 16
 17 解释一下下面内容：
 18 1、集合数相等为什么说明了去掉当前结点是没什么影响
 19 当你标记一个点之后，在进行并查集这个时候肯定会把这个点孤立出来，也就是多了一个只有这一个点的集合
 20 如果在原图中这个点就被孤立，那么标记之后还是相当于孤立，那么这个时候去掉当前结点是没什么影响
 21
 22 2、前面完整结点的集合数+1=当前集合数时为什么说明了去掉当前结点是没什么影响
 23 如果这个点原本并不在原图中孤立，那么如果标记这个点之后，如果这个点去掉不会造成影响，那么标记这个点之后的集合数要比
 24 之前的大1
 25 */
 26 #include<stdio.h>
 27 #include<string.h>
 28 #include<iostream>
 29 #include<algorithm>
 30 #include<queue>
 31 using namespace std;
 32 const int maxn=505;
 33 int n,m;
 34 struct node
 35 {
 36     int u,v;
 37 } e[5005];
 38 int vist[550],fa[550];
 39 int Find(int x)
 40 {
 41     return x==fa[x]?fa[x]:Find(fa[x]);
 42 }
 43 void Union(int x,int y)
 44 {
 45     int xc=Find(x);
 46     int yc=Find(y);
 47     if(xc!=yc)
 48     {
 49         fa[xc]=yc;
 50     }
 51 }
 52 int main()
 53 {
 54     int k;
 55     int u,v;
 56     while(scanf("%d%d",&n,&m)!=EOF)
 57     {
 58         for(int i=0; i<n; i++)
 59             fa[i]=i;
 60         for(int i=0; i<m; i++)
 61         {
 62             scanf("%d%d",&u,&v);
 63             e[i].u=u,e[i].v=v;
 64             Union(u,v);
 65         }
 66         int num=0,num1;
 67         for(int i=0; i<n; i++)
 68         {
 69             if(fa[i]==i)
 70             {
 71                 num++;
 72             }
 73         }
 74         memset(vist,0,sizeof(vist));
 75         scanf("%d",&k);
 76         while(k--)
 77         {
 78             num1=0;
 79             for(int i=0;i<n;i++)
 80                 fa[i]=i;
 81             int x;
 82             scanf("%d",&x);
 83             vist[x]=1;
 84             for(int i=0;i<m;i++)
 85             {
 86                 if(vist[e[i].u]==1||vist[e[i].v]==1)
 87                 continue;
 88                 else
 89                     Union(e[i].u,e[i].v);
 90             }
 91             for(int i=0;i<n;i++)
 92                 if(fa[i]==i)
 93                 num1++;
 94             if(num==num1||num+1==num1)
 95             printf("City %d is lost.\n",x);
 96             else
 97                 printf("Red Alert: City %d is lost!\n",x);
 98             num=num1;
 99         }
100         num=0;
101         for(int i=0;i<n;i++)
102             if(vist[i]==1)
103             num++;
104         if(num==n)
105             printf("Game Over.\n");
106     }
107     return 0;
108 }