Codeforces Round #652 (Div. 2) D. TediousLee（dp）

题目链接：https://codeforces.com/contest/1369/problem/D

题意

最初有一个结点，衍生规则如下：

• 如果结点 $u$ 没有子结点，添加 $1$ 个子结点
• 如果结点 $u$ 有 $1$ 个子结点，添加 $2$ 个子结点
• 如果结点 $u$ 有 $3$ 个子结点，跳过该结点

如：

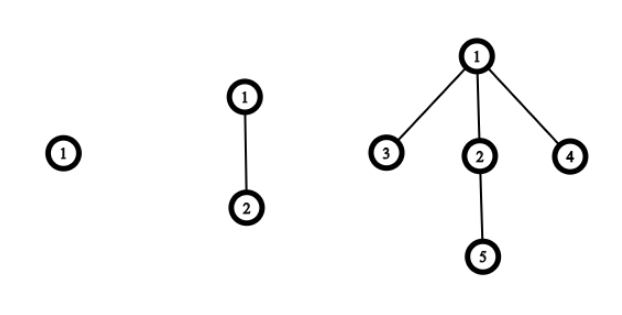
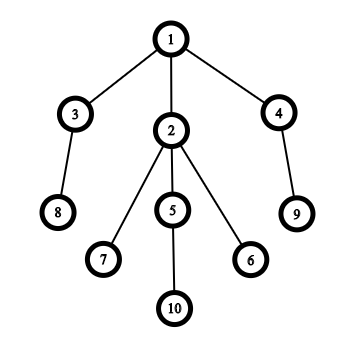
\begin{equation} level = 1, 2, 3,4 \end{equation}

爪形结构如下：

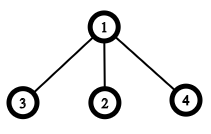
问可以在 $level_n$ 选出几个互不相交的爪形结构。

题解

衍生的过程是具有重复性的，最终变化的是根结点 $1$ 下的三棵子树，左右两棵子树为 $level_{n - 2}$，中间的子树为 $level_{n - 1}$ 。

因为 $level_1$ 和 $level_2$ 的根结点并未使用，所以可以在 $level_3$ 中选择以根结点 $1$ 为中心的爪形结构。

同理，$level_4$、$level_5$ 可以通过选取较下层的爪形结构来避免根结点的使用，所以在 $level_6$ 中又可以选取以根结点 $1$ 为中心的爪形结构。

即，$level$ 为 $3$ 的倍数的图形都可以再额外选取位于根结点的爪形结构。

综上，设 $dp_i$ 为 $level_i$ 中最多可选出的互不相交的爪形结构个数，有递推式：

\begin{equation} dp_i = 2 \times dp_{i - 2} + dp_{i - 1} + (i\ \%\ 3 == 0) \end{equation}

代码

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e6 + 10;
constexpr int mod = 1e9 + 7;

int dp[N];

void init() {
    dp[1] = dp[2] = 0;
    dp[3] = dp[4] = 1;
    for (int i = 5; i < N; i++)
        dp[i] = (2LL * dp[i - 2] + dp[i - 1] + (i % 3 == 0)) % mod;
}

void solve() {
    int n; cin >> n;
    cout << 4LL * dp[n] % mod << "\n";
}

int main() {
    init();
    int t; cin >> t;
    while (t--) solve();
}