poj1470 Closest Common Ancestors [ 离线LCA tarjan ]

传送门

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 14915		Accepted: 4745

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form:

nr_of_vertices 
vertex:(nr_of_successors) successor1 successor2 ... successorn 
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form: 
nr_of_pairs 
(u v) (x y) ...

The input file contents several data sets (at least one). 
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
For example, for the following tree: 

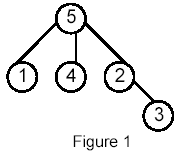
Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint

Huge input, scanf is recommended.

Source

Southeastern Europe 2000

 

 

万分感谢万能的kss，几句话就教会了窝，以下题意及题解均转自kss博客：

http://blog.csdn.net/u011645923/article/details/35780547

 

题意：给定一个n个结点的有向树，m次询问（u,v）的 lca,输出询问中作为lca的点以及作为lca的次数。

思路：离线lca ,利用tarjan算法。

tarjan算法的步骤是(当dfs到节点u时):
1. 在并查集中建立仅有u的集合,设置该集合的祖先为u
2. 对u的每个孩子v:
   2.1 tarjan之
   2.2 合并v到父节点u的集合,确保集合的祖先是u
3. 设置u为已遍历
4. 处理关于u的查询,若查询(u,v)中的v已遍历过,则LCA(u,v)=v所在的集合的祖先

14006525

njczy2010

1470

Accepted

2992K

516MS

G++

1979B

2015-03-25 19:29:20

 #include <cstdio>
 #include <cstring>
 #include <stack>
 #include <vector>
 #include <algorithm>

 #define ll long long
 int const N = ;
 int const M = ;
 int const inf = ;
 ll const mod = ;

 using namespace std;

 int n,m;
 vector<int> bian[N];
 vector<int> query[N];
 int cnt[N];
 int fa[N];
 int vis[N];
 int degree[N];

 int findfa(int x)
 {
     return fa[x] == x ? fa[x] : fa[x] = findfa(fa[x]);
 }

 void ini()
 {
     int i,j;
     int k,u,v;
     memset(cnt,,sizeof(cnt));
     memset(vis,,sizeof(vis));
     memset(degree,,sizeof(degree));
     for(i=;i<=n;i++){
         bian[i].clear();
         query[i].clear();
         fa[i]=i;
     }
     for(i=;i<=n;i++){
         scanf("%d:(%d)",&u,&k);
         for(j=;j<k;j++){
             scanf("%d",&v);
             bian[u].push_back(v);
             degree[v]++;
         }
     }
     scanf("%d",&m);
     for(i=;i<=m;i++){
         while(getchar()!='(') ;
         scanf("%d%d",&u,&v);
         while(getchar()!=')') ;
         query[u].push_back(v);
         query[v].push_back(u);
     }
 }

 void tarjan(int u,int f)
 {
     vector<int>::iterator it;
     int v;
     for(it=bian[u].begin();it!=bian[u].end();it++){
         v=*it;
         tarjan(v,u);
     }

     for(it=query[u].begin();it!=query[u].end();it++){
         v=*it;
         if(vis[v]==) continue;
         cnt[ findfa(v) ]++;
     }
     vis[u]=;
     fa[u]=f;
 }

 void solve()
 {
     int i;
     for(i=;i<=n;i++){
         if(degree[i]==){
             tarjan(i,-);
         }
     }
 }

 void out()
 {
     int i;
     for(i=;i<=n;i++){
          //   printf("%d:%d\n",i,cnt[i]);
         if(cnt[i]!=){
             printf("%d:%d\n",i,cnt[i]);
         }
     }
 }

 int main()
 {
     //freopen("data.in","r",stdin);
     //scanf("%d",&T);
    // for(cnt=1;cnt<=T;cnt++)
     //while(T--)
     while(scanf("%d",&n)!=EOF)
     {
         ini();
         solve();
         out();
     }
 }