[codeforces494B]Obsessive String

[codeforces494B]Obsessive String

试题描述

Hamed has recently found a string t and suddenly became quite fond of it. He spent several days trying to find all occurrences of t in other strings he had. Finally he became tired and started thinking about the following problem. Given a string s how many ways are there to extract k ≥ 1 non-overlapping substrings from it such that each of them contains string t as a substring? More formally, you need to calculate the number of ways to choose two sequences a₁, a₂, ..., a_k and b₁, b₂, ..., b_ksatisfying the following requirements:

• k ≥ 1
• 
• 
• 
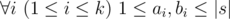
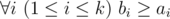
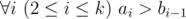
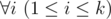•   t is a substring of string s_{a_i}s_{a_i + 1}... s_{b_i} (string s is considered as 1-indexed).

As the number of ways can be rather large print it modulo 10⁹ + 7.

输入

Input consists of two lines containing strings s and t (1 ≤ |s|, |t| ≤ 10⁵). Each string consists of lowercase Latin letters.

输出

Print the answer in a single line.

输入示例

welcometoroundtwohundredandeightytwo
d

输出示例

数据规模及约定

见“输入”

题解

首先用 KMP 预处理一波数组 pos[i]，表示串 s 第 i 位左边最靠右的那次对于 t 的完整匹配的左端点（有点拗口，举个栗子 s = "ababa"，那么 pos[i] = {0, 0, 1, 1, 3}）。

有了 pos 数组，就可以 dp 了。我们考虑每个位置放置一个左端点，或是一个右端点，或者不放（注意不放有两种情况，一种是刚放完左端点，一种是刚放完右端点）；于是设 f[i][0] 表示最后一次放的是左端点，放在了位置 i 或者 i 的左边；f[i][1] 表示最后一次放的是右端点，放在了位置 i 或 i 的左边。转移时就是考虑当前这个位置放置还是不放，具体转移方程留给读者思考。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;

int read() {
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

#define maxn 100010
#define MOD 1000000007

char S[maxn], T[maxn];
int Fail[maxn], pos[maxn], f[maxn][2];

int main() {
	scanf("%s%s", S + 1, T + 1);

	int n = strlen(S + 1), m = strlen(T + 1);
	for(int i = 2; i <= m + 1; i++) {
		int j = Fail[i-1];
		while(j > 1 && T[j] != T[i-1]) j = Fail[j];
		Fail[i] = T[j] == T[i-1] ? j + 1 : 1;
	}
	int p = 1;
	for(int i = 1; i <= n; i++) {
		while(p > 1 && T[p] != S[i]) p = Fail[p];
		p = T[p] == S[i] ? p + 1 : 1;
		if(p == m + 1) pos[i] = i - m + 1;
	}
	for(int i = 1; i <= n; i++) if(!pos[i]) pos[i] = pos[i-1];
//	for(int i = 1; i <= n; i++) printf("%d%c", pos[i], i < n ? ' ' : '\n');
	f[0][1] = 1;
	for(int i = 1; i <= n; i++) {
		f[i][0] = (f[i-1][0] + f[i-1][1]) % MOD;
		f[i][1] = (f[i-1][1] + (pos[i] ? f[pos[i]][0] : 0)) % MOD;
//		printf("(%d, %d)%c", f[i][0], f[i][1], i < n ? ' ' : '\n');
	}

	printf("%d\n", (f[n][1] ? f[n][1] : MOD) - 1);

	return 0;
}