BZOJ3732: Network(Kruskal重构树)

题意

Link

给出一张$n$个点的无向图，每次询问两点之间边权最大值最小的路径

$n \leqslant 15000, m \leqslant 30000, k \leqslant 20000$

Sol

很显然答案一定在最小生成树上，但是此题还有一个更为玄学的做法—Kruskal重构树

它是在Kruskal算法上改进而来的。

算法流程：

1. 对于此题来说，将边权从小到大排序
2. 用并查集维护两点的联通性，若祖先不相同，那么新建一个节点，权值为边权。左右儿子分别为两个点

这样建出来的树，我们称之为Kruskal重构树

它有许多美妙的性质

• 是一颗二叉树
• 两点的LCA的点权为原图中最大值最小的路径上的最大值
• 任意点的权值大于左右儿子的权值，是一个大根堆

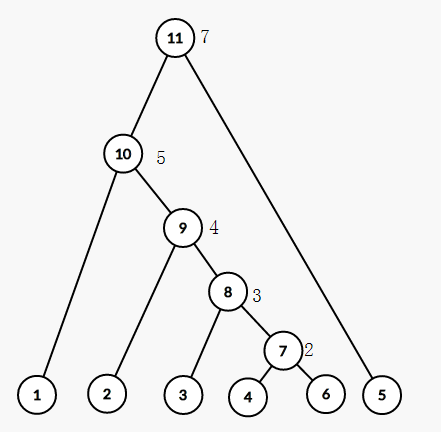
对于此题的样例来说，建出来的图大概长这样

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 1e5 + , INF = 1e9, B = ;
inline int read() {
    char c = getchar(); int x = , f = ;
    while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * f;
}
int fa[MAXN], f[MAXN][], ch[MAXN][], cnt, val[MAXN], deep[MAXN];
int N, M, K;
struct Edge {
    int u, v, w;
    bool operator < (const Edge &rhs) const {
        return w < rhs.w;
    }
}E[MAXN];
int head[MAXN], num = ;
inline void AddEdge(int x, int y, int z) {
    E[++num] = (Edge){x, y, z};
}
int find(int x) {
    if(fa[x] == x) return fa[x];
    else return fa[x] = find(fa[x]);
}
void Kruskal() {
    sort(E + , E + num + );
    int tot = ;
    for(int i = ; i <= M; i++) {
        int x = E[i].u, y = E[i].v;
        int fx = find(x), fy = find(y);
        if(fx == fy) continue;
        ch[++cnt][] = fx, ch[cnt][] = fy;
        fa[fa[x]] = fa[fa[y]] = f[fa[x]][] = f[fa[y]][] = cnt;
        val[cnt] = E[i].w;

    }
}
void dfs(int x) {
    if(!ch[x][] && !ch[x][]) return ;
    deep[ch[x][]] = deep[ch[x][]] = deep[x] + ;
    dfs(ch[x][]); dfs(ch[x][]);
}
int LCA(int x, int y) {
    if(deep[x] < deep[y]) swap(x, y);
    for(int i = B; i >= ; i--)
        if(deep[f[x][i]] >= deep[y])
            x = f[x][i];
    if(x == y) return x;
    for(int i = B; i >= ; i--)
        if(f[x][i] != f[y][i])
            x = f[x][i], y = f[y][i];
    return f[x][];
}
main() {
    //freopen("a.in", "r", stdin);
    cnt = N = read(); M = read(); K = read();
    for(int i = ; i <= N << ; i++) fa[i] = i;
    for(int i = ; i <= M; i++) {
        int x = read(), y = read(), z = read();
        AddEdge(x, y, z);
    }
    Kruskal();
    deep[cnt] = ; dfs(cnt);
    for(int i = ; i <= B; i++)
        for(int j = ; j <=  * N; j++)
            f[j][i] = f[f[j][i - ]][i - ];
    while(K--) {
        int  x = read(), y = read();
    //    printf("%d\", LCA(x, y));
        printf("%d\n", val[LCA(x, y)]);
    }
    return ;
}