Classification week2: logistic regression classifier 笔记
华盛顿大学 machine learning: Classification 笔记。
linear classifier 线性分类器

多项式:

Logistic regression & 概率模型

P(y = +1 | x) = ?
使用 logistic函数

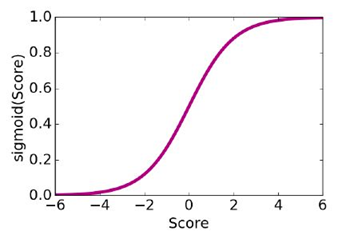
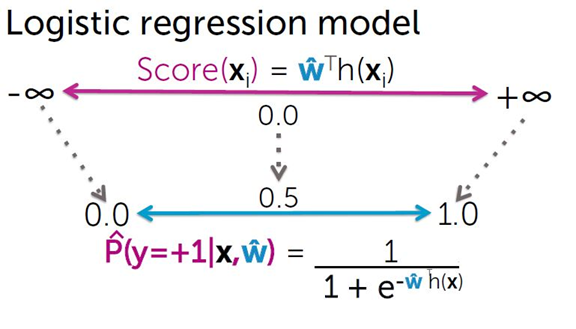
这个概率模型怎么来的?
(李航《统计学习方法》)

即
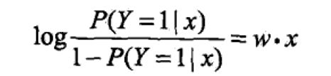
考虑对输入x进行分类的线性函数 w x,其值域为实数域,线性函数wx可转换为概率:
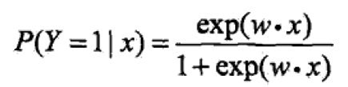
这时,线性函数值越接近正无穷,概率值就越接近1;线性函数值越接近负无穷,
概率值就越接近0。
这种概率描述适用于这样的情况:即在P=0或P=1附近,P对X的变化不敏感。这种概率模型的应用场景主要是分类。
极大似然估计模型参数w
Maximize Likelihood Estimation(MLE) 极大似然估计

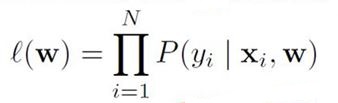
即 选择使 l(w) 最大的参数 w。
对 l(w) 取对数:

展开得
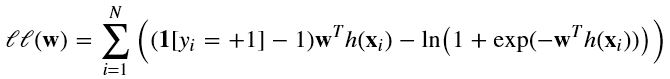
梯度下降(Gradient-descent):

防止过拟合:

即
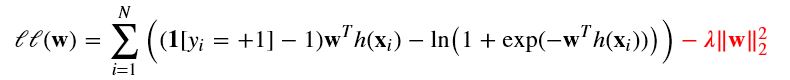
梯度下降
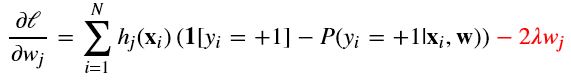
Classification week2: logistic regression classifier 笔记的更多相关文章
- 学习Logistic Regression的笔记与理解(转)
学习Logistic Regression的笔记与理解 1.首先从结果往前来看下how logistic regression make predictions. 设我们某个测试数据为X(x0,x1, ...
- 李宏毅机器学习笔记3:Classification、Logistic Regression
李宏毅老师的机器学习课程和吴恩达老师的机器学习课程都是都是ML和DL非常好的入门资料,在YouTube.网易云课堂.B站都能观看到相应的课程视频,接下来这一系列的博客我都将记录老师上课的笔记以及自己对 ...
- Classification and logistic regression
logistic 回归 1.问题: 在上面讨论回归问题时.讨论的结果都是连续类型.但假设要求做分类呢?即讨论结果为离散型的值. 2.解答: 假设: 当中: g(z)的图形例如以下: 由此可知:当hθ( ...
- 机器学习算法笔记1_2:分类和逻辑回归(Classification and Logistic regression)
形式: 採用sigmoid函数: g(z)=11+e−z 其导数为g′(z)=(1−g(z))g(z) 如果: 即: 若有m个样本,则似然函数形式是: 对数形式: 採用梯度上升法求其最大值 求导: 更 ...
- 分类和逻辑回归(Classification and logistic regression)
分类问题和线性回归问题问题很像,只是在分类问题中,我们预测的y值包含在一个小的离散数据集里.首先,认识一下二元分类(binary classification),在二元分类中,y的取值只能是0和1.例 ...
- Logistic Regression学习笔记
1.李航<统计学习方法>: 2.https://blog.csdn.net/laobai1015/article/details/78113214 3.http://www.cnblogs ...
- 机器学习技法笔记:05 Kernel Logistic Regression
Roadmap Soft-Margin SVM as Regularized Model SVM versus Logistic Regression SVM for Soft Binary Clas ...
- Logistic Regression Using Gradient Descent -- Binary Classification 代码实现
1. 原理 Cost function Theta 2. Python # -*- coding:utf8 -*- import numpy as np import matplotlib.pyplo ...
- 深度学习 Deep LearningUFLDL 最新Tutorial 学习笔记 2:Logistic Regression
1 Logistic Regression 简述 Linear Regression 研究连续量的变化情况,而Logistic Regression则研究离散量的情况.简单地说就是对于推断一个训练样本 ...
随机推荐
- Vue实例总结
一.登陆框的要点总结: 1.暂无数据就是要myData里没数据时候才出来:删除全部就是要有数据才出来.v-show的使用: 2.表格行就是需要循环数据,v-for.{{$index}}.{{item. ...
- sql where 1=1和 0=1 的作用(多条件查询错误的问题)
where 1=1; 这个条件始终为True,在不定数量查询条件情况下.1=1能够非常方便的规范语句. 一.不用where 1=1 在多条件查询中的困扰 举个样例,假设您做查询页面,而且.可查询的 ...
- IStorage
IStorage 接口支持结构化存储对象的创建和管理. 结构化存储允许分层存储在单个文件的信息,和通常被称为“文件系统内文件”. 元素的结构化存储对象存储和小溪. 存储类似于目录,和流类似于文件. 在 ...
- C# 中 in,out,ref 的作用与区别
In:过程不会改写In的内容 Out和out:传入的值不会被过程所读取,但过程可以写 ref:传入的值,过程会读,也会写 就象你把布料送到裁缝的一个收料箱(裁缝用这个区别是哪家客户) IN:这块布料, ...
- JAVA加解密 -- 对称加密算法与非对称加密算法
对称加密算法:双方必须约定好算法 DES 数据加密标准:由于不断地被破解 自98年起就已经逐渐放弃使用 AES 目前使用最多的加密方式,官方并未公布加密方式已被破解,替代DES 实现和DES非常接近 ...
- 爪哇国新游记之十九----使用Stack检查数字表达式中括号的匹配性
/** * 辅助类 * 用于记载字符和位置 * */ class CharPos{ char c; int pos; public CharPos(char c,int pos){ this.c=c; ...
- diskpart分盘代码
List Disk Select Disk 0 Clean Create Partition Primary Size=512000 Active Format Quick Create Partit ...
- 深入理解C/C++ [Deep C (and C++)] (2)
好.接着深入理解C/C++之旅.我在翻译第一篇的时候.自己是学到不不少东西,因此打算将这整个ppt翻译完成. 请看以下的代码片段: #include <stdio.h> void foo( ...
- Subl 命令
Subl 是sublime 的命令 添加环境变量后可以,在cmd 或者git 下直接 使用subl 进行 打开sublime Example: Subl 打开编辑器 Subl . 将当 ...
- Android Exception 16(Error in ADT 23 Update)
http://stackoverflow.com/questions/24445367/error-in-adt-23-update http://stackoverflow.com/question ...
