ACM-ICPC 2018 徐州赛区网络预赛 G. Trace【树状数组维护区间最大值】

任意门：https://nanti.jisuanke.com/t/31459

There's a beach in the first quadrant. And from time to time, there are sea waves. A wave ( xx , yy ) means the wave is a rectangle whose vertexes are ( 00 , 00 ), ( xx , 00 ), ( 00 , yy ), ( xx , yy ). Every time the wave will wash out the trace of former wave in its range and remain its own trace of ( xx , 00 ) -> ( xx , yy ) and ( 00 , yy ) -> ( xx , yy ). Now the toad on the coast wants to know the total length of trace on the coast after n waves. It's guaranteed that a wave will not cover the other completely.

Input

The first line is the number of waves n(n \le 50000)n(n≤50000).

The next nn lines，each contains two numbers xx yy ,( 0 < x0<x , y \le 10000000y≤10000000 )，the ii-th line means the ii-th second there comes a wave of ( xx , yy ), it's guaranteed that when 1 \le i1≤i , j \le nj≤n ，x_i \le x_jxi≤xj and y_i \le y_jyi≤yj don't set up at the same time.

Output

An Integer stands for the answer.

Hint：

As for the sample input, the answer is 3+3+1+1+1+1=103+3+1+1+1+1=10

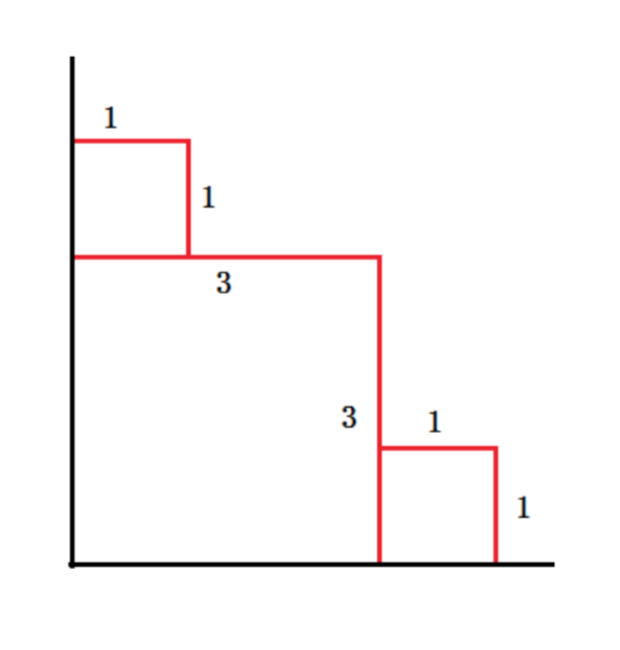
样例输入复制

样例输出复制

题意概括：

有 N 个矩形海浪（给出右上角坐标），后一个海浪会覆盖前一个海浪，求可见的海浪轮廓长度和。

解题思路：

按照从后往前遍历海浪（因为后面的会把前面的海浪覆盖），每次当前海浪的坐标分别减去当前海浪区间的最大值（x轴记录y的最大值， y值记录x的最大值）。

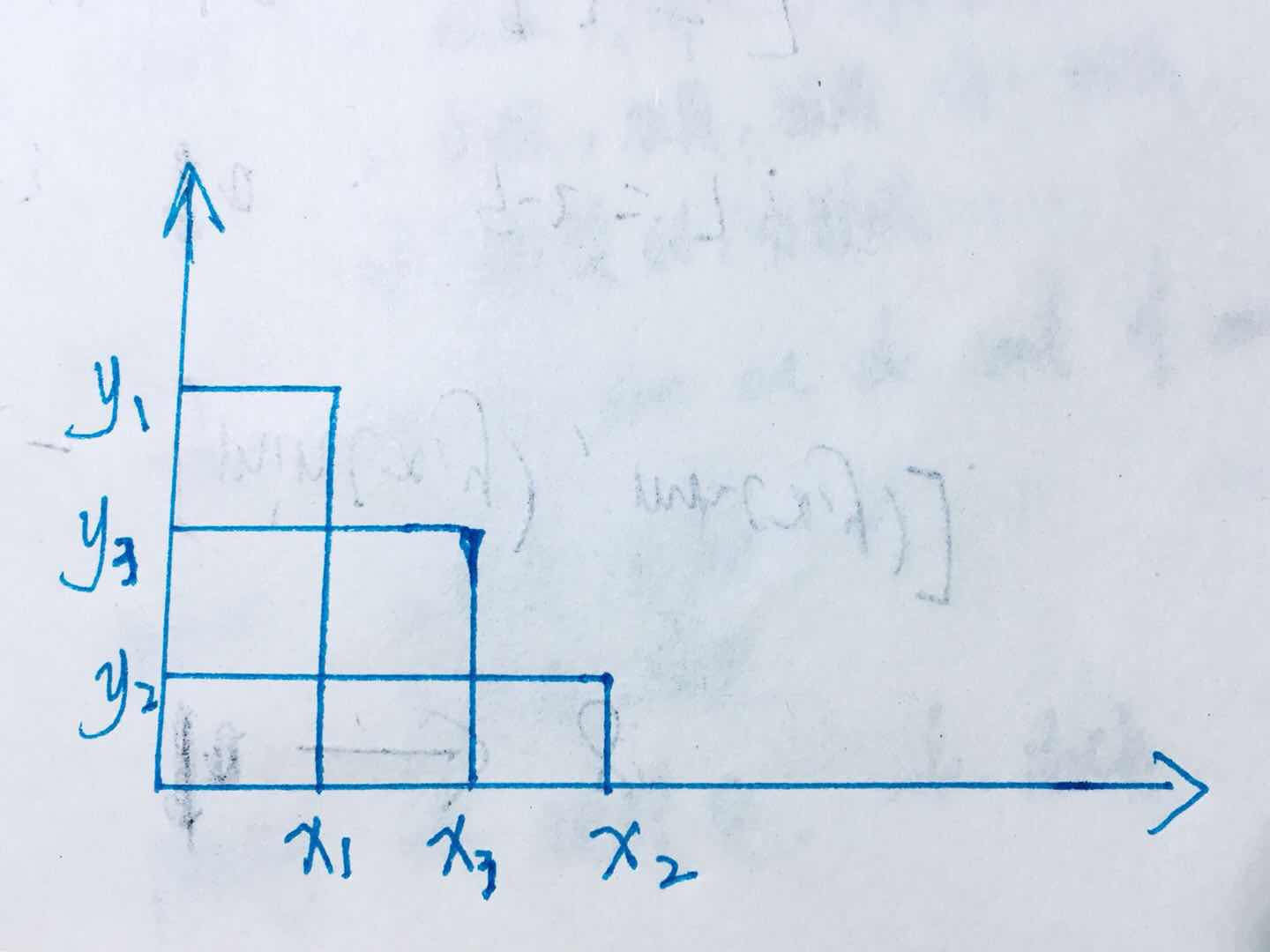
举个上面的栗子：

注意顺序是从后往前扫。

所以第一个是 x3，y3

0~x3 最大的 y 是 0 所以第一条可见轮廓为 y3 - 0;

0~y3 的最大 x 是 0 所以第二条可见轮廓为 x3 - 0;

分别更新这两段的最大值（用两个树状数组维护即可，只更新【0， X】和【0，Y】这两个区间！！！）

第二个是 x2, y3

0 ~ x2 最大的 y 是 0 ！！！（因为前面只更新到 x3）所以第三条可见轮廓为 y2 - 0；

0 ~ y2 最大的 x 是 x3 所以第四条可见轮廓为 x2 - x3；

更新区间；

第三个是 x1 y1

0~x1 最大的 y3 是 0 所以第五条可见轮廓为 y1 - y3;

0~y1 的最大 x3 是所以第六条可见轮廓为 x1 - x3;

更新区间；

AC code：

 #include <bits/stdc++.h>

 #define INF 0x3f3f3f3f

 #define LL long long

 using namespace std;

 const int MAXN = 5e4+;

 LL res_x, res_y, ans;

 LL t[MAXN*];

 LL y[MAXN*];

 int N;

 struct date

 {

     LL x, y;

 }wape[MAXN];

 LL lowbit(LL x)

 {

     return x&(-x);

 }

 void add(LL x ,LL val, int no)

 {

     for(LL i = x; i > ; i-=lowbit(i)){

         if(no == ) t[i] = max(t[i], val);

         else y[i] = max(y[i], val);

     }

 }

 LL query(LL x, int no)

 {

     LL res = ;

     for(LL i = x; i < MAXN*; i+=lowbit(i)){

         if(no == ) res = max(res, t[i]);

         else res = max(res, y[i]);

     }

     return res;

 }

 int main()

 {

     scanf("%d", &N);

     for(int i = ; i <= N; i++){

         scanf("%lld%lld", &wape[i].x, &wape[i].y);

     }

     for(int i = N; i > ; i--){

         res_y = wape[i].y - query(wape[i].x, );

         if(res_y > ) ans+=res_y;

         res_x = wape[i].x - query(wape[i].y, );

         if(res_x > ) ans+=res_x;

         add(wape[i].x, wape[i].y, );

         add(wape[i].y, wape[i].x, );

     }

     printf("%lld\n", ans);

     return ;

 }