HDU 4587 TWO NODES（割点）（2013 ACM-ICPC南京赛区全国邀请赛）

Description

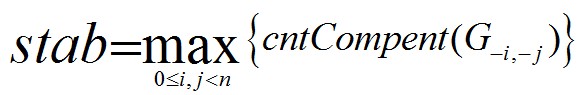Suppose that G is an undirected graph, and the value of stab is defined as follows: Among the expression,G _{-i, -j} is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes. cntCompent is the number of connected components of X independently.  Thus, given a certain undirected graph G, you are supposed to calculating the value of stab.

 

Input

The input will contain the description of several graphs. For each graph, the description consist of an integer N for the number of nodes, an integer M for the number of edges, and M pairs of integers for edges (3<=N,M<=5000).  Please note that the endpoints of edge is marked in the range of [0,N-1], and input cases ends with EOF.

 

Output

For each graph in the input, you should output the value of stab.

题目大意：给一个n个点m条边的无向图，删掉任意两个点，求最大联通分量数。

思路：枚举要被删掉的第一个点，然后用tarjan求剩下的每一个点被删掉后能增加的联通分量数。根据dfs的性质，有多少个分支的lowu ≥ pre[u]，删掉u后就有多少个联通分量，删掉第一个点的时候剩下的块数加上删掉第二个点的联通分量数，就是删掉第一个点可以获得的最大连通分量数。要注意的是，如果要删掉的点是一个孤立的点，那么它的连通分量数反而会减少。时间复杂度为O(nm)，12S可以承受。

代码（5000MS）：

 #include <iostream>
 #include <cstdio>
 #include <cmath>
 #include <cstring>
 using namespace std;

 const int MAXN = ;
 const int MAXE = MAXN * ;

 int head[MAXN];
 int to[MAXE], next[MAXE];
 int pre[MAXN], cut[MAXN];
 int n, m, dfs_clock, ecnt, stab;

 void init() {
     memset(head, , sizeof(head));
     ecnt = ;
 }

 void add_edge2(int u, int v) {
     to[ecnt] = v; next[ecnt] = head[u]; head[u] = ecnt++;
     to[ecnt] = u; next[ecnt] = head[v]; head[v] = ecnt++;
 }

 int del;

 int dfs(int u, int fa) {
     int lowu = pre[u] = ++dfs_clock;
     for(int p = head[u]; p; p = next[p]) {
         int &v = to[p];
         if(v == del) continue;
         if(!pre[v]) {
             int lowv = dfs(v, u);
             lowu = min(lowu, lowv);
             if(lowv >= pre[u]) ++cut[u];
         } else if(pre[v] < pre[u] && v != fa) {
             lowu = min(lowu, pre[v]);
         }
     }
     if(fa < ) --cut[u];
     return lowu;
 }

 int main() {
     while(scanf("%d%d", &n, &m) != EOF) {
         init();
         while(m--) {
             int a, b;
             scanf("%d%d", &a, &b);
             add_edge2(a, b);
         }
         stab = ;
         for(int i = ; i < n; ++i) {
             del = i;
             int sum = ;
             memset(pre, , sizeof(pre));
             memset(cut, , sizeof(cut));
             dfs_clock = ;
             for(int u = ; u < n; ++u) {
                 if(u == i || pre[u]) continue;
                 ++sum;
                 dfs(u, -);
             }
             int maxcut = -;
             for(int u = ; u < n; ++u) if(u != i)
                 maxcut = max(maxcut, cut[u]);
             stab = max(stab, sum + maxcut);
         }
         printf("%d\n", stab);
     }
 }