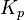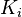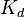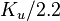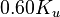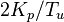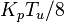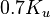上面一篇文章讲了一下PID算法中的三个常量大致的在PID算法中起的一个作用，但在实际的使用中，究竟应该如何调节（或者用更加专业的话说是整定）PID控制算法的三个。首先可以将KP，KI，KD三个常量全部设为一，观察一下系统的调节情况是不是过快。大致确定输出控制量的结果需要右移多少位来做最终的控制量。然后将KI，KD设为0，KP从0一直逐渐增加试探，直到被控制量有一定超调，且有一定的小震荡。此时kp算调节到差不多了。我们可以继续调节Ki，通过增大Ki使被控制量最终平稳下来的值尽可能是我们设定的值。积分量ki的调节与Kp的调节相似，从小到大调整。但要注意ki的增加会使得超调量变大，所以ki增大时kp应当相应减小一点。调节完KP与Ki之后的效果就是有一定超调，但最终还是能基本稳定在设定值，最后我们就开始调节Kd。依旧是从小到大调整，通过kd的调节能使超调尽量减小。

PID控制算法还有一种调节方式——齐格勒－尼科尔斯方法。

其调试方式为，首先将积分和微分增益设置为0，然后比例增益从零开始逐渐增加，直到到达极限增益KU，此时控制器输出值以恒定值振荡。KU和振荡周期TU根据不同的类型，按下表中的方式来设置比例、积分和微分增益。

Ziegler–Nichols方法[2]
控制类型
比例 - -
比例-积分 -
经典比例-积分-微分（PID）[3]
Pessen Integral Rule[3]
some overshoot[3]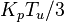

--维基百科 http://zh.wikipedia.org/wiki/Ziegler%E2%80%93Nichols%E6%96%B9%E6%B3%95

看上去 会比第一种会简单的多。但现在有个问题就是Ku究竟是该调整到一个什么样的值。

自己不负责任的理解：Ku应该是设定ki与kd全为0时调整kp的值，使得被控制量出现等幅震荡时此时的kp即ku。

wiki上还有提到其他两种方法，没怎么仔细看，有时间再去研究研究。

本篇结束，刚刚开始学pid，表示文章中一定有不少错漏之处。希望各位童鞋批评指正。

下篇（目测最后一篇）把自己写的pid控制算法的代码放上来给大伙瞅瞅吧。。

杂谈PID控制算法——第二篇：调·三个量的更多相关文章

  1. 杂谈PID控制算法——第一篇：三个量

    电赛训练了大半个暑假,人渐渐开始进入到了疲倦期.既然这样那就好好休息下自己也好吧. 休息也不能光休息,乘机把平常写过的一些东西好好整理也好. 从第一次训练开始我们就接触到了一个新的名词——PID控制理 ...

  2. 杂谈PID控制算法——最终篇：C语言实现51单片机中的PID算法

    真遗憾,第二篇章没能够发表到首页上去.趁热打铁.把最终篇——代码篇给发上来. 代码的设计思想请移步前两篇文章 //pid.h #ifndef __PID__ #define __PID__ /*PID ...

  3. 第三篇——第二部分——第三文 配置SQL Server镜像——域环境

    原文:第三篇--第二部分--第三文 配置SQL Server镜像--域环境 原文出处:http://blog.csdn.net/dba_huangzj/article/details/28904503 ...

  4. Spring第二篇和第三篇的补充【JavaConfig配置、c名称空间、装载集合、JavaConfig与XML组合】

    前言 在写完Spring第二和第三篇后,去读了Spring In Action这本书-发现有知识点要补充,知识点跨越了第二和第三篇,因此专门再开一篇博文来写- 通过java代码配置bean 由于Spr ...

  5. angularjs学习第三天笔记（过滤器第二篇---filter过滤器及其自定义过滤器）

    您好,我是一名后端开发工程师,由于工作需要,现在系统的从0开始学习前端js框架之angular,每天把学习的一些心得分享出来,如果有什么说的不对的地方,请多多指正,多多包涵我这个前端菜鸟,欢迎大家的点 ...

  6. PID控制算法的C语言实现

    参考: PID控制器开发笔 浅谈位置式PID 专家PID控制在快速系统中的仿真及应用(这篇了论文介绍的积分分离PID.专家PID(脚本实现和simulink实现)很详细) PID控制算法的C语言实现一 ...

  7. [转]PID控制算法原理

    PID控制算法是工业界使用极其广泛的一个负反馈算法,相信这个算法在做系统软件时也有用武之处,这里摘录了知乎上的一篇文章,后面学习更多后自己总结一篇 以下为原文: PID控制应该算是应用非常广泛的控制算 ...

  8. PID控制算法的简单分析和仿真！

    PID算法简单剖析如下: 1.首先我们来看一下PID系统的基本组成模块: 如图所示,图中相关参数的表示如下: r(t):系统实际上需要的输出值,这是一个标准值,在我们设定了之后让这个系统去逼近的一个值 ...

  9. PHP 性能分析第二篇: Xhgui In-Depth

    [前言]这是国外知名博主 Davey Shafik 撰写的 PHP 应用性能分析系列的第二篇,第一篇介绍 Xhprof/Xhgui,第三篇则关注于性能调优实践. 在第一篇中,我们初步介绍了 xhpro ...

随机推荐

  1. 如何打开小米，oppo，华为等手机的系统应用的指定页面

    如题,拿Oppo 手机做个示例,小米 华为也是如此. 在编写Android应用的时候,我们经常会有这样的需求,我们想直接打开系统应用的某个页面.比如在Oppo R9 手机上我们想打开某个应用的通知管理 ...

  2. [bzoj1015][JSOI2008]星球大战——并查集+离线处理

    题解 给定一张图,支持删点和询问连通块个数 按操作顺序处理的话要在删除点的同时维护图的形态(即图具体的连边情况),这是几乎不可做的 我们发现,这道题可以先读入操作,把没删的点的边先连上,然后再倒序处理 ...

  3. algorithm ch7 QuickSort

    快速排序是基于分治模式的排序,它将数组a[p,...,r]分成两个子数组a[p,...q-1],a[q+1,...,r],使得a[p,...,q-1]中每个元素都小于a[q],而且小于等于a[q+1, ...

  4. Linux下安装mantis配置指南【转】

    转自:http://blog.csdn.net/xabc3000/article/details/6858229 目录(?)[-] Linux下安装mantis配置指南 配置Linux下的Apache ...

  5. phpstorm调试环境XDebug搭建

    1.安装XDebug,通过phpinfo()可以看到xdebug是否已安装!!!如果未安装,可以先看我的另一篇关于XDebug安装的文章:http://www.cnblogs.com/cxscode/ ...

  6. Mac-item+zsh

    $brew cask install iterm2 $ sh -c "$(curl -fsSL https://raw.github.com/robbyrussell/oh-my-zsh/m ...

  7. 获取span中的值

    js-code:var baseinfoallfeesum=$("#allFeeSum").html(); $("#baseInfoAllFeeSum").va ...

  8. HTML5初学---坦克大战基础

    让小球动起来,根据键盘的W(上),D(右),S(下),A(左):键的点击移动小球 <!DOCTYPE html> <html> <head> <meta ch ...

  9. javascript 将字符串当函数执行

    //语法 eval(str); //demo var t = "func"; eval(''+func+'()');

  10. hdu5829

    多校训练8,有官方题解 主要之前没写过ntt,感觉不是很懂原根 先贴一份当模板吧 #include<iostream> #include<cstdio> #include< ...