洛谷 P3381【模板】最小费用最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

输出格式：

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

输入输出样例

输入样例#1：

输出样例#1：

50 280

说明

时空限制：1000ms,128M

（BYX：最后两个点改成了1200ms）

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=5000，M<=50000

样例说明：

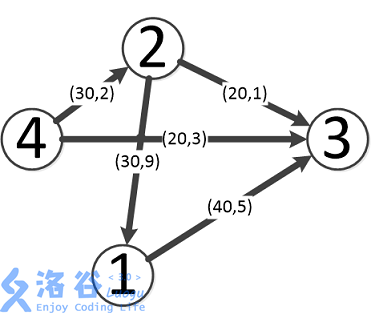
如图，最优方案如下：

第一条流为4-->3，流量为20，费用为3*20=60。

第二条流为4-->2-->3，流量为20，费用为（2+1）*20=60。

第三条流为4-->2-->1-->3，流量为10，费用为（2+9+5）*10=160。

故最大流量为50，在此状况下最小费用为60+60+160=280。

故输出50 280。

思路：费用流的模板题，就是在最大流中用 spfa或dijkstra等算法来代替，不同的是费用流在管流量的同时也要管边权，所以，可以说算是最大流的升级版吧，我目前还只会 spfa版本的，dijkstra的还不太会写。

代码：

#include<cstdio>

#include<cstring>

#include<cctype>

#include<queue>

#define maxn 5007

using namespace std;

int num=1,n,m,head[maxn],pre[maxn],dis[maxn],vis[maxn],maxflow,ans,S,T;

const int inf=0x3f3f3f3f;

inline int qread() {

  char c=getchar();int num=0,f=1;

  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;

  for(;isdigit(c);c=getchar()) num=num*10+c-'0';

  return num*f;

}

struct node {

  int u,v,f,w,nxt;

}e[maxn*20];

inline void ct(int u, int v, int f, int w) {

  e[++num]=node{u,v,f,w,head[u]};

  head[u]=num;

}

inline bool bfs() {

  memset(vis,0,sizeof(vis));

  memset(dis,0x3f,sizeof(dis));

  queue<int>q;

  q.push(S),dis[S]=0;

  while(!q.empty()) {

    int u=q.front();

    q.pop();

    vis[u]=0;

    for(int i=head[u];i;i=e[i].nxt) {

      int v=e[i].v,f=e[i].f;

      if(dis[v]>dis[u]+e[i].w&&f) {

        dis[v]=dis[u]+e[i].w;

        pre[v]=i;

        if(!vis[v]) {

          vis[v]=1;

          q.push(v);

        }

      }

    }

  }

  return dis[T]!=inf;

}

inline void work() {

  int minn=inf;

  for(int i=T;i!=S;i=e[pre[i]].u)

    minn=min(minn,e[pre[i]].f);

  for(int i=T;i!=S;i=e[pre[i]].u) {

    e[pre[i]].f-=minn;

    e[pre[i]^1].f+=minn;

    ans+=minn*e[pre[i]].w;

  }

  maxflow+=minn;

}

int main() {

  n=qread(),m=qread(),S=qread(),T=qread();

  for(int i=1;i<=m;++i) {

    int u=qread(),v=qread(),f=qread(),w=qread();

    ct(u,v,f,w),ct(v,u,0,-w);

  }

  while(bfs()) work();

  printf("%d %d\n",maxflow,ans);

  return 0;

}