[codeforces 360]A. Levko and Array Recovery

[codeforces 360]A. Levko and Array Recovery

试题描述

Levko loves array a₁, a₂, ... , a_n, consisting of integers, very much. That is why Levko is playing with array a, performing all sorts of operations with it. Each operation Levko performs is of one of two types:

1. Increase all elements from l_i to r_i by d_i. In other words, perform assignments a_j = a_j + d_i for all j that meet the inequation l_i ≤ j ≤ r_i.
2. Find the maximum of elements from l_i to r_i. That is, calculate the value .

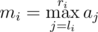Sadly, Levko has recently lost his array. Fortunately, Levko has records of all operations he has performed on array a. Help Levko, given the operation records, find at least one suitable array. The results of all operations for the given array must coincide with the record results. Levko clearly remembers that all numbers in his array didn't exceed 10⁹ in their absolute value, so he asks you to find such an array.

输入

The first line contains two integers n and m (1 ≤ n, m ≤ 5000) — the size of the array and the number of operations in Levko's records, correspondingly.

Next m lines describe the operations, the i-th line describes the i-th operation. The first integer in the i-th line is integer t_i (1 ≤ t_i ≤ 2) that describes the operation type. If t_i = 1, then it is followed by three integers l_i, r_i and d_i (1 ≤ l_i ≤ r_i ≤ n,  - 10⁴ ≤ d_i ≤ 10⁴) — the description of the operation of the first type. If t_i = 2, then it is followed by three integers l_i, r_i and m_i (1 ≤ l_i ≤ r_i ≤ n, - 5·10⁷ ≤ m_i ≤ 5·10⁷) — the description of the operation of the second type.

The operations are given in the order Levko performed them on his array.

输出

In the first line print "YES" (without the quotes), if the solution exists and "NO" (without the quotes) otherwise.

If the solution exists, then on the second line print n integers a₁, a₂, ... , a_n (|a_i| ≤ 10⁹) — the recovered array.

输入示例

输出示例

YES
   

数据规模及约定

见“输入”

题解

对于每一个 t_i = 1 的操作，我们把对应区间的懒标记暴力地加上；然后对于一个 t_i = 2 的操作，我们可以知道这个区间中每一个数的上限。然后把所有上限的效果叠加（即取最小值）就是答案序列。注意最后再判断一下得到的序列是否能满足所有操作，如果不能就无解。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <map>
#include <set>
using namespace std;

const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
    if(Head == Tail) {
        int l = fread(buffer, 1, BufferSize, stdin);
        Tail = (Head = buffer) + l;
    }
    return *Head++;
}
int read() {
    int x = 0, f = 1; char c = getchar();
    while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
    while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}

#define maxn 5010
#define maxq 5010
#define oo 1000000000
int n, q, addv[maxn], lim[maxn], A[maxn];
struct Que {
	int tp, l, r, d;
	Que() {}
	Que(int _1, int _2, int _3, int _4): tp(_1), l(_2), r(_3), d(_4) {}
} qs[maxq];

int main() {
	n = read(); q = read();
	for(int i = 1; i <= n; i++) lim[i] = oo;
	for(int i = 1; i <= q; i++) {
		int t = read(), l = read(), r = read(), d = read();
		qs[i] = Que(t, l, r, d);
		if(t == 1)
			for(int j = l; j <= r; j++) addv[j] += d;
		if(t == 2)
			for(int j = l; j <= r; j++) lim[j] = min(lim[j], d - addv[j]);
	}

	for(int i = 1; i <= n; i++) A[i] = lim[i];
	for(int i = 1; i <= q; i++) {
		if(qs[i].tp == 1)
			for(int j = qs[i].l; j <= qs[i].r; j++) A[j] += qs[i].d;
		if(qs[i].tp == 2) {
			int mx = -oo;
			for(int j = qs[i].l; j <= qs[i].r; j++) mx = max(mx, A[j]);
			if(mx != qs[i].d) return puts("NO"), 0;
		}
	}

	puts("YES");
	for(int i = 1; i <= n; i++) printf("%d%c", lim[i], i < n ? ' ' : '\n');

	return 0;
}