svm 之 线性可分支持向量机

定义：给定线性可分训练数据集，通过间隔最大化或等价的求解凸二次规划问题学习获得分离超平面和分类决策函数，称为线性可分支持向量机。

目录：

• 函数间隔

• 几何间隔

• 间隔最大化

• 对偶算法

1、函数间隔

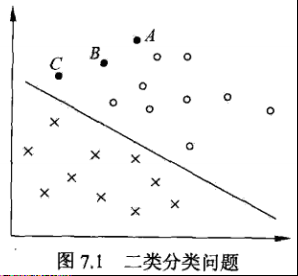
考虑分类算法的两个方面：确信度 + 正确性

确信度：用点到分离超平面的距离表示，间接表示为$w ⋅x_i+b$，分类的结果有多大的自信保证它是正确的；

正确性：$y_i$  与 $w ⋅x_i+b$的符号是否一致，表征分类是否正确；

结合以上两点，

某一实例点的函数间隔的定义即：$γ ̂_i= y_i (w⋅x_i+b)$；

训练数据集的函数间隔定义为：$γ ̂*=min\quadγ ̂*_i$；

确信度：$w⋅x_i+b$可以间接的表示点到超平面的距离，距离越小，说明确信度越低，反之；

正确性：当 $y_i$  与 $w⋅x_i+b$ 的符号一致时，函数间隔为正，此时分类是正确的，反之，分类错误；

2、几何间隔

但是.........

当w,b成倍的变化，变成了ℷw,ℷb时，超平面没有发生变化，但是函数间隔却变化了 ℷ 倍，基于此，

某一实例点的几何间隔就被定义为：$γ_i=y_i\frac{(w⋅x_i+b)}{‖w‖}$；

训练数据集的几何间隔定义为：$γ=min⁡\quadγ_i$；

几何间隔不会随着w和b的比例变化而同比例的变化；

而且，$\frac{(w⋅x_i+b)}{‖w‖}$    也是点到超平面真正的距离（不再是间接的表示了），所以几何间隔其实是带符号的距离；

几何间隔和函数间隔之间的关系：$γ=\frac{γ^*}{‖w‖}$

3、间隔最大化

线性可分支持向量机的目的是：正确的分离超平面 + 最大的几何间隔

最大的几何间隔直观的解释：以最大的确信度分离数据集，即使是最难分的实例点也可以被分的很好（大的确信度）；

最大化几何间隔：

$max\quadγ$  ；

$s.t.\quad\frac{(y_i (w⋅x_i+b))}{‖w‖} ≥γ ,\qquad i=1,2……N$ ；

带入函数间隔：

$max\quad\frac{γ^*}{‖w‖}$ ；

$s.t.\quad y_i (w⋅x_i+b)≥γ^*, \qquad  i=1,2……N$；

考虑上优化问题，可知$γ^*$ 的取值不会影响优化问题（当w和b成比例变化时，$γ^*$也会成比例变化，优化问题不变），可取$γ^*$ 为1，又可知最大化 $\frac1{‖w‖}$   等价与最小化 $\frac1{2} ‖w‖^2$，故优化问题就可以写成一个凸二次规划问题：

$min\quad\frac⁡{1}{2} ‖w‖^2$ ；

$s.t. \quad y_i (w⋅x_i+b)≥1 ,\qquad i=1,2…N$；

算法：线性可分支持向量机学习算法 -- 最大间隔算法

输入：训练数据集 $T{(x_1,y_1 ),(x_2,y_2 ),…,(x_n,y_n )}  ,  x∈R^n  ,  y∈ \left \{ +1,-1 \right \} $；

输出：分离超平面和分类决策函数；

（1）构造并求解凸二次规划问题：

$min⁡\quad\frac1{2} ‖w‖^2$ ；

$s.t.\quad y_i (w⋅x_i+b)≥1 , \qquad i=1,2…N$；

得到问题的解：$w^∗, b^∗ $  ;

（2）得到分离超平面：$w^∗⋅x+b^∗=0$ ；

分类决策函数：$f(x)=sign(w^∗⋅x+b^∗ )$；

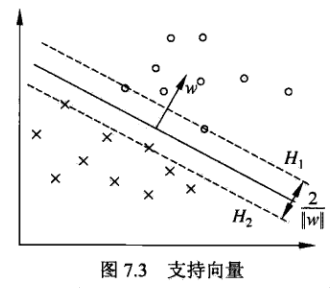
支持向量：距离超平面最近的实例点，（那些最难分类的实例点）

间隔边界：

$H_1  : w⋅x+b=1$；

$H_2  : w⋅x+b=−1$；

4、对偶算法

根据拉格朗日对偶性，求对偶问题即可求原始问题。对偶问题一般更容易求解。

构建拉格朗日函数：$L(w,b,α)=\frac1{2} ‖w‖^2−∑α_i y_i (w⋅x_i+b)+∑α_i $；

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题：max⁡  min⁡  L(w,b,α)

（1）求解极小问题 ⁡min⁡ L(w,b,α)   分别对w和b求导：

$\frac{\partial L(w,b,\alpha)}{\partial w}=w-\sum_{i=1}^N\alpha_iy_ix_i=0$           ;            $\frac{\partial L(w,b,\alpha)}{\partial b}=-\sum_{i=1}^N\alpha_iy_i=0$

得到：

$w=\sum_{i=1}^N\alpha_iy_ix_i$；

$\sum_{i=1}^N\alpha_iy_i=0$；

带入到极小问题中：

$min\quad L(w,b,α)=-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot{x_j})+\sum_{i=1}^N\alpha_i$

（2）求解极大问题：max⁡ min⁡ L(w,b,α)

$max\quad-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot{x_j})+\sum_{i=1}^N\alpha_i$

$s.t.\quad\sum_{i=1}^N\alpha_iy_i=0 , \alpha_i\geqslant 0,i=1,2,...,N$

等价于：

$min\quad\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot{x_j})-\sum_{i=1}^N\alpha_i$

$s.t.\quad\sum_{i=1}^N\alpha_iy_i=0 , \alpha_i\geqslant 0,i=1,2,...,N$

我们的原始问题是：

$min\quad \frac1{2} ‖w‖^2$    ；

$s.t. \quad y_i (w⋅x_i+b)≥1$；

原始问题满足定理C.3(统计机器学习附录)的条件，故可以通过求解对偶问题来求解原始问题；

定理：设$α^∗$ 是对偶问题的解，则存在$α_j>0$，按下式求原始问题的解：

$w^∗=∑α_i^∗ y_i x_i$；

$b^∗=y_j−∑α_i^∗ y_i (x_i⋅x_j )$；

证明：

根据KKT的互补条件：$α_i c_i (x)=0，若α_j>0，则c_j (x)=0；y_j (w⋅x_j+b)−1=0≫  y_j^2 (w⋅x_j+b)−y_j=0≫b=y_j−w⋅x_j$

至此，就得到了分离超平面和分类决策函数。

算法：线性可分支持向量机 -- 对偶学习算法

输入：训练数据集 $T{(x_1,y_1 ),(x_2,y_2 ),…,(x_n,y_n )}  ,  x∈R^n  ,  y ∈ \left \{ +1,-1 \right \} $ ；

输出：分离超平面和分类决策函数；

（1）构造并求解原始问题的对偶问题：

$min\quad\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot{x_j})-\sum_{i=1}^N\alpha_i$

$s.t.\quad\sum_{i=1}^N\alpha_iy_i=0 , \alpha_i\geqslant 0,i=1,2,...,N$

得到解为$α^∗$；

（2）根据对偶问题的解求原始问题的解：

$w^∗=∑α_i^∗ y_i x_i$；

$b^∗=y_j−∑α_i^∗ y_i (x_i⋅x_j )$；

（3）得到分离超平面和分类决策函数；

支持向量：$α_i^∗>0$的实例点，

根据KKT互补条件，对于$α_i^∗>0$的实例点，$y_j (w⋅x_j+b)−1=0 ≫ w⋅x_j+b=±1$  ，即实例点在间隔边界上，这个定义和之前的定义是一致的；

至此，线性可分支持向量机完结。

但是...........

线性可分支持向量机（硬间隔最大化）针对的是线性可分训练数据集，然而，现实世界里有很多数据集是线性不可分的（样本数据中有噪声或特异点），这种情况下改怎么办？