hdu6578 2019湖南省赛D题Modulo Nine 经典dp

@

目录

• 题目
• 解析
• AC_Code

题目

---

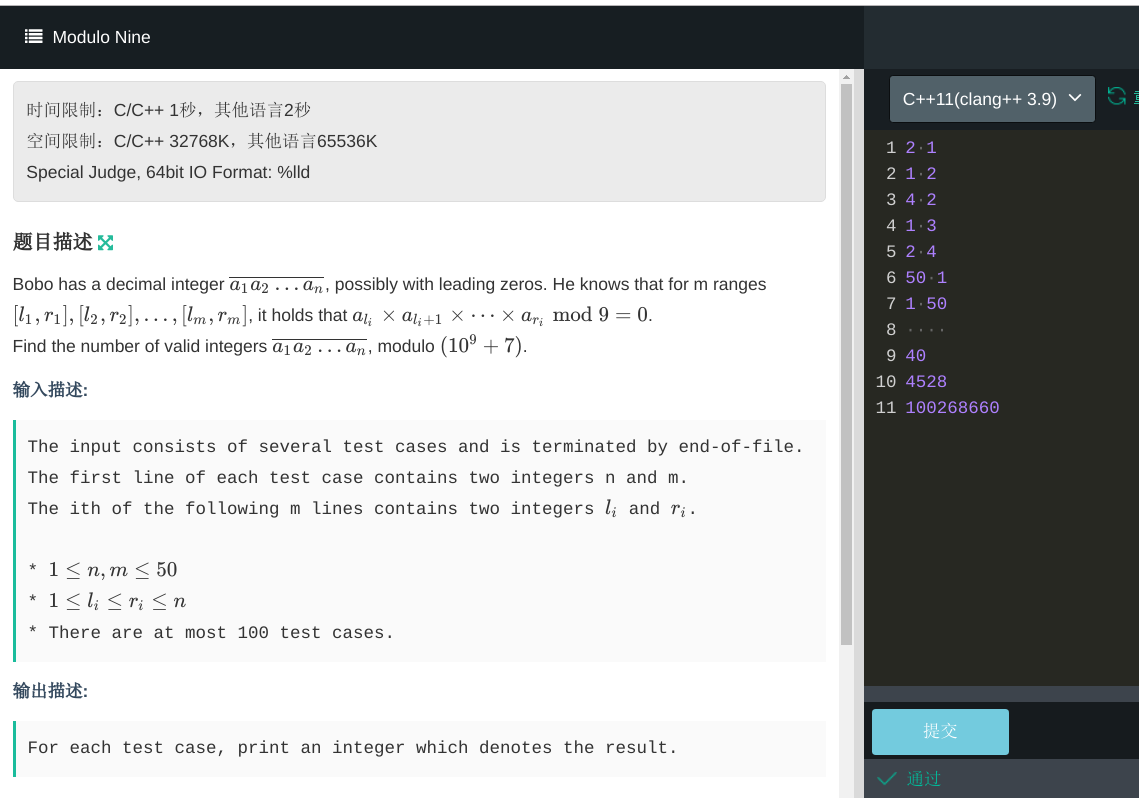
第一题题意是一共有{0,1,2,3}四种数字供选择，问有多少个长度为n的序列满足所有m个条件，每个条件是说区间[L,R]内必须有恰好x个不同的数字。

第二题题意是10个数字供选择，问有多少个长度为n的序列满足所有m个条件，每个条件是说区间[L,R]数字的乘积必须是9的倍数。

解析

• hdu6578
• \(dp[t][i][j][k]\)表示填完前\(t\)个位置，{\(0,1,2,3\)}中出现的数字最后一次出现的位置排序后为\(t,i,j,k(t\gt i\gt j\gt k)\)的方案数。\(0\)表示数字未出现。
• 枚举四种转移：
• 填\(t-1\)位置的数字：\(dp[t][i][j][k]\)
• 填\(i\)位置的数字：\(dp[t][t-1][j][k]\)
• 填\(j\)位置的数字：\(dp[t][t-1][i][k]\)
• 填\(k\)位置的数字：\(dp[t][t-1][i][j]\)
• 但是不是所有转移都有效，所以要枚举限制条件，将不合法的转移pass掉
• 枚举所有终点在\(t\)点的限制条件，将不合法的转移的\(dp\)值归零。
• 时间复杂度：\(O(n^4)\)，滚动数组优化空间复杂度：\(O(n^3)\)

---

• 2019湖南省赛D题Modulo Nine
• 关于乘积是否是9的倍数，这里只有3类数字，0和9表示两个3，3和6表示一个3，其他表示零个3
• \(dp[t][i][j]\)表示填完前\(t\)个位置，最后一个3在\(i\)，倒数第二个3在\(j\)的方案数。
• 枚举3种转移：
• 填\(0或9\)：\(dp[t][t][t]\)
• 填\(3或6\)：\(dp[t][t][i]\)
• 填其他数字：\(dp[t][i][j]\)
• 但是不是所有转移都有效，所以要枚举限制条件，将不合法的转移pass掉
• 枚举所有终点在\(t\)点的限制条件，将不合法的转移的\(dp\)值归零。
• 时间复杂度：\(O(n^3)\)，滚动数组优化空间复杂度：\(O(n^2)\)

---

两题思路一模一样，是一种很经典的dp。

AC_Code

hdu6578
const int mod = 998244353;
const int MXN = 1e5 + 7;
const int MXE = 2e5 + 7;

int n, m, c;
vector<pii> mp[MXN];
LL dp[2][101][101][101];
void get_dp() {
    dp[c][0][0][0] = 1;
    for(int t = 1; t <= n; ++t) {
        c ^= 1;
        for(int i = 0; i <= t; ++i) for(int j = 0; j <= i; ++j) for(int k = 0; k <= j; ++k) dp[c][i][j][k] = 0;
        for(int i = 0; i < t; ++i) for(int j = 0; j <= i; ++j) for(int k = 0; k <= j; ++k) {
            if((i != j && j != k) || k == 0) {
                dp[c][i][j][k] = (dp[c][i][j][k] + dp[c ^ 1][i][j][k]) % mod;
                dp[c][t - 1][j][k] = (dp[c][t - 1][j][k] + dp[c ^ 1][i][j][k]) % mod;
                dp[c][t - 1][i][j] = (dp[c][t - 1][i][j] + dp[c ^ 1][i][j][k]) % mod;
                dp[c][t - 1][i][k] = (dp[c][t - 1][i][k] + dp[c ^ 1][i][j][k]) % mod;
            }
        }
        for(int h = 0; h < (int)mp[t].size(); ++h) {
            int l = mp[t][h].fi, x = mp[t][h].se;
            for(int i = 0; i < t; ++i) for(int j = 0; j <= i; ++j) for(int k = 0; k <= j; ++k) {
                int cnt = 1;
                if(i >= l) ++ cnt;
                if(j >= l) ++ cnt;
                if(k >= l) ++ cnt;
                if(cnt != x) dp[c][i][j][k] = 0;
            }
        }
    }
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("/home/cwolf9/CLionProjects/ccc/in.txt", "r", stdin);
    //freopen("/home/cwolf9/CLionProjects/ccc/out.txt", "w", stdout);
#endif
    int tim = read();
    while(tim --) {
        n = read(), m = read();
        for(int i = 1, a, b, c; i <= m; ++i) {
            a = read(), b = read(), c = read();
            mp[b].eb(mk(a, c));
        }
        get_dp();
        LL ans = 0;
        for(int i = 0; i < n; ++i)
            for(int j = 0; j <= i; ++j)
                for(int k = 0; k <= j; ++k) if((i != j && j != k) || k == 0) ans = (ans + dp[c][i][j][k]) % mod;
        printf("%lld\n", (ans+mod)%mod);
        for(int i = 0; i <= n; ++i) mp[i].clear();
    }
#ifndef ONLINE_JUDGE
    cout << "time cost:" << clock() << "ms" << endl;
#endif
    return 0;
}

2019省赛D
const int mod = 1e9 + 7;
const int MXN = 1e5 + 7;
const int MXE = 2e5 + 7;

int n, m, c;
int mp[MXN];
LL dp[2][101][101];
void get_dp() {
    clr(dp, 0);
    dp[c][0][0] = 1;
    for(int t = 1; t <= n; ++t) {
        c ^= 1;
        for(int i = 0; i <= t; ++i) for(int j = 0; j <= i; ++j) dp[c][i][j] = 0;
        for(int i = 0; i <= t; ++i) {
            for(int j = 0; j <= i; ++j) {
                dp[c][i][j] = (dp[c][i][j] + dp[c^1][i][j] * 6) % mod;
                dp[c][t][i] = (dp[c][t][i] + dp[c^1][i][j] * 2) % mod;
                dp[c][t][t] = (dp[c][t][t] + dp[c^1][i][j] * 2) % mod;
            }
        }
        if(mp[t] == -1) continue;
        for(int i = 0; i <= t; ++i) {
            for(int j = 0; j <= i; ++j) {
                if(i < mp[t] || j < mp[t]) dp[c][i][j] = 0;
            }
        }
    }
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("/home/cwolf9/CLionProjects/ccc/in.txt", "r", stdin);
    //freopen("/home/cwolf9/CLionProjects/ccc/out.txt", "w", stdout);
#endif
    int tim = 1;
    while(~scanf("%d%d", &n, &m)) {
        for(int i = 1; i <= n; ++i) mp[i] = - 1;
        for(int i = 1, a, b; i <= m; ++i) {
            a = read(), b = read();
            mp[b] = big(mp[b], a);
        }
        get_dp();
        LL ans = 0;
        for(int i = 0; i <= n; ++i) for(int j = 0; j <= i; ++j) ans = (ans + dp[c][i][j]) % mod;
        printf("%lld\n", (ans + mod) % mod);
    }
#ifndef ONLINE_JUDGE
    cout << "time cost:" << clock() << "ms" << endl;
#endif
    return 0;
}