cygwin的用途

cgywin简介

打开cygwin的官方网站（www.cygwin.com），一行英文非常醒目：Get that Linux feeling – on Windows!

简而言之，cygwin是一个在windows平台上运行的unix模拟环境，是一个感觉用起来像是linux环境的工具集。也就是说，在cygwin上你可以执行诸多linux命令，不仅如此，也可以执行windows DOS下的命令程序。

但要注意的是，cygwin并不能直接运行在linux中运行的程序，必须在cygwin中重新编译该程序源码后才能让该程序在windows中运行。

cgywin是cygnus solutions公司开发的自由软件。cygnus是一个伟大的公司，开发了很多流行的开源软件。比如eCos、gcc编译器等等。现在它被Red Hat收购了。

cygwin安装

网上有很多介绍如何安装cygwin的文章。其实我觉得参照cygwin官方网站上的介绍就可以了。所以我是采用在线安装的方法来安装cygwin的。

后记补充：cygwin默认安装在C盘的根目录下。我电脑C盘没空间，所以把它安装在E盘。据有网友反映，cygwin安装在哪个盘关系不大，但应该安装在NTFS格式的盘，否则有可能产生一些莫名其妙的问题（就我自己而言，目前为止碰到了一个问题：解压交叉编译工具包时出现了不能建立硬连接，从而导致不能正常安装交叉编译器）。所以，在这里建议：如果你的C盘有足够空间，那就安装在C盘，如果没有则选择一个NTFS格式的盘，选择安装在盘的根目录下。

1. 下载setup-x86.exe文件，先确定你的windows是32-bit还是64-bit，然后去http://cygwin.com/install.html下载对应的setup-x86.exe文件。

2. 接下来就像安装windows其它软件一样，双击setup-x86.exe进行一步一步的安装。

选择安装方式：有3种选择：第1是选择在线安装方式；第2是下载安装包但不安装；第3种是本地安装。如下左图所示。

 

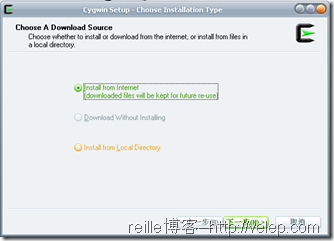
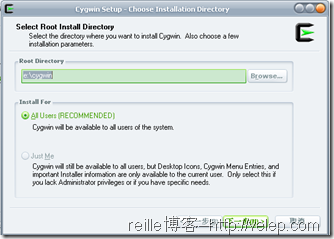
3. 选择cygwin的安装路径，默认是c:/cygwin，如上右图所示。

4. 选择cygwin安装包的路径。如果是在线安装或只下载cygwin安装包，则用于存放下载下来的cygwin安装包。如下左图所示。

 

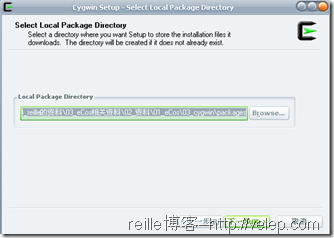
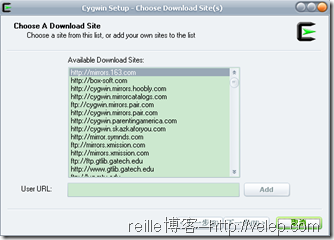
5. 选择一个镜像站点。在中国，选择163镜像站点就可以了，如上右图所示。

6. 选择安装包。我安装里，没有去选择，直接用default来安装。如下图所示。

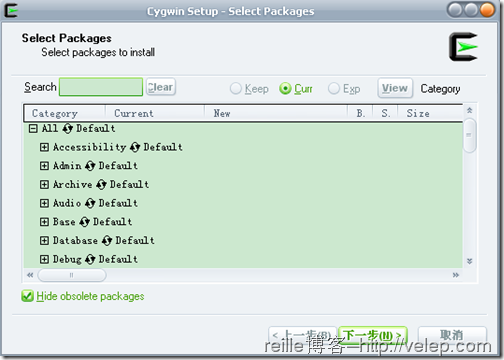
点击下一步后，会显示关联的安装包，这可以不用管，就接下一步就OK了。最后就是等待下载并安装完成了。

7. 把cygwin安装路径下的bin目录添加到环境变量中，如下右图所示。这样，就可以直接在cmd.exe里面使用Linux命令了，比如less, cat, wc , wget。

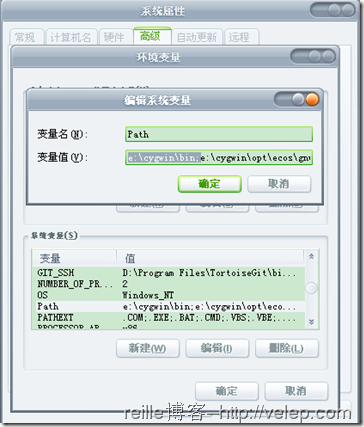
cygwin使用

对于用户而言，cygwin其实就是个shell，即命令终端界面，在其中可以执行linux的命令。

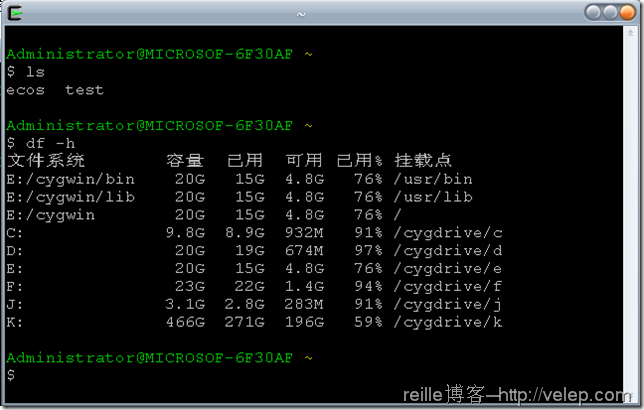
cygwin把它的安装路径作为linux环境中的根目录/，并把windows下的盘挂到/cygdrive/目录下，如上图所示。所以，在cygwin中访问windows下的资料文档就很方便了。

再来看下cygwin安装下的东西，如下图所示：

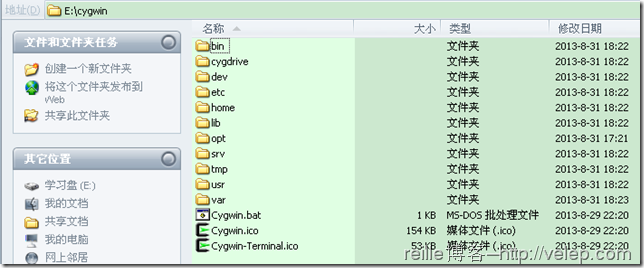
是不是很熟悉，目录结构就是linux的，如dev、bin、etc、home、lib、opt、tmp、var、usr等。

在cgywin界面中，点击右键，选择options…，如下图所示。

在这个界面中，可对cygwin的参数进行配置，如显示文本、快捷键、窗口等参数进行配置。

转载自：http://velep.com/archives/747.html