【JZOJ 3909】Idiot 的乘幂

题面:

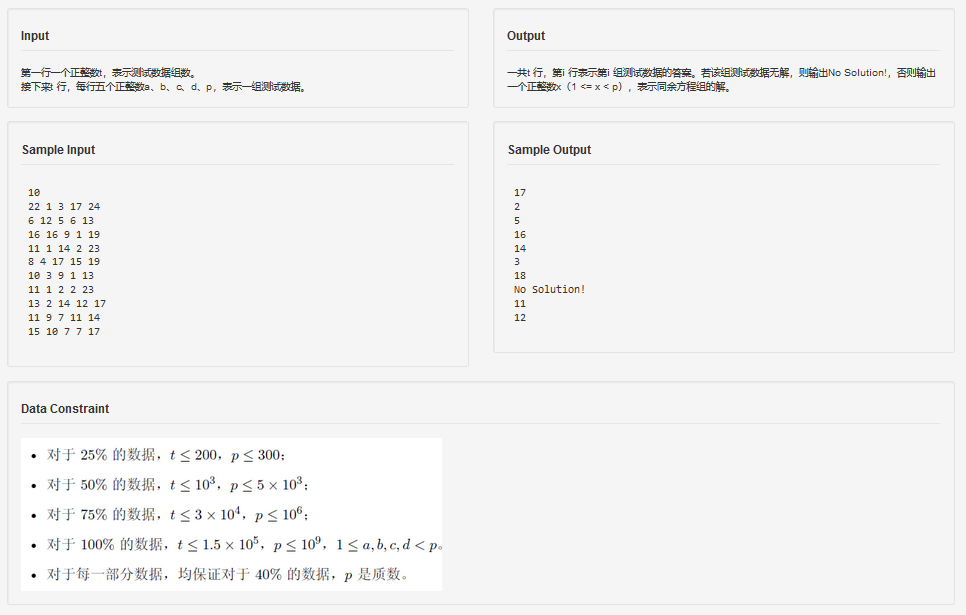
正文：

把题目中的方程组组合在一起就变成了：

\(X^{a+c}\equiv b \cdot d (\mod p)\)

那这时，我们假定两个数\(x\)和\(y\)，使得：

\(ax + cy = 1\)

于是：

\(X^{ax+cy}\equiv X \equiv b^x \cdot d^y (\mod p)\)

那我们就可以根据\(ax+cy=1\)跑一遍扩欧，再根据\(X \equiv b^x \cdot d^y (\mod p)\)，就能得出\(X\)了。

---

但是，你以为出题人这么善良吗？

\(x\)和\(y\)可能是负数，做\(b^x \cdot d^y\) 时就相当于 \(\frac{1}{b^{(-x)}} \cdot \frac{1}{d^{(-y)}}\), 因为有膜法技能同余，这里肯定出锅。

所以我们还要给\(b\)和\(d\)求个逆元，同样，也是用扩欧。