[luogu]P1600 天天爱跑步[LCA]

[luogu]P1600

[NOIP 2016]天天爱跑步

题目描述

小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。«天天爱跑步»是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。

这个游戏的地图可以看作一一棵包含n个结点和n−1条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从1到n的连续正整数。

现在有m个玩家,第i个玩家的起点为Si​,终点为Ti​ 。每天打卡任务开始时,所有玩家在第0秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)

小C想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点j的观察员会选择在第Wj​秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第Wj​秒也理到达了结点 j 。 小C想知道每个观察员会观察到多少人?

注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点j作为终点的玩家: 若他在第Wj​秒前到达终点,则在结点j的观察员不能观察到该玩家;若他正好在第Wj​秒到达终点,则在结点j的观察员可以观察到这个玩家。

输入输出格式

输入格式：

第一行有两个整数n和m 。其中n代表树的结点数量, 同时也是观察员的数量, m代表玩家的数量。

接下来n−1行每行两个整数u和v,表示结点u到结点v有一条边。

接下来一行n个整数,其中第j个整数为Wj​ ,
表示结点j出现观察员的时间。

接下来m行,每行两个整数Si​,和Ti​,表示一个玩家的起点和终点。

对于所有的数据,保证1≤Si​,Ti​≤n,0≤Wj​≤n 。

输出格式：

输出1行n个整数,第j个整数表示结点j的观察员可以观察到多少人。

输入输出样例

输入样例1#：

6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6

输出样例1#：

2 0 0 1 1 1

输入样例2#：

5 3
1 2
2 3
2 4
1 5
0 1 0 3 0
3 1
1 4
5 5

输出样例2#：

1 2 1 0 1

说明

【样例1说明】

对于1号点，W_i=0Wi​=0，故只有起点为1号点的玩家才会被观察到，所以玩家1和玩家2被观察到，共有2人被观察到。

对于2号点，没有玩家在第2秒时在此结点，共0人被观察到。

对于3号点，没有玩家在第5秒时在此结点，共0人被观察到。

对于4号点，玩家1被观察到，共1人被观察到。

对于5号点，玩家1被观察到，共1人被观察到。

对于6号点，玩家3被观察到，共1人被观察到。

【子任务】

每个测试点的数据规模及特点如下表所示。 提示: 数据范围的个位上的数字可以帮助判断是哪一种数据类型。

（图还是来自luogu）

---

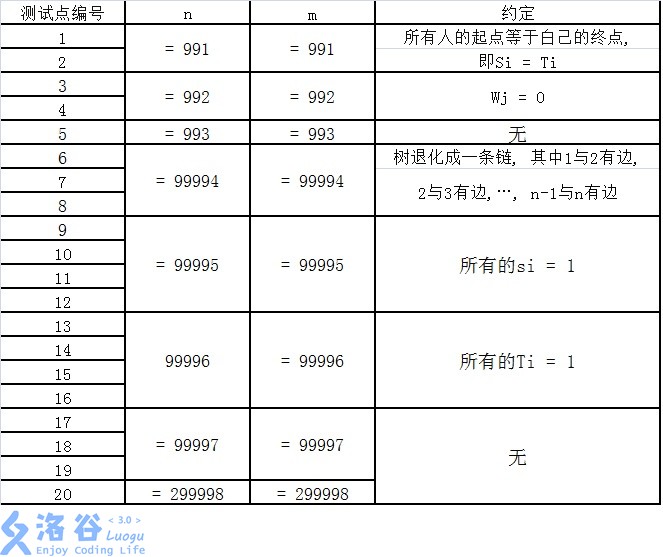
今天总算搞懂了NOIP2016 day1 t2 running。

根据ysy大佬的代码，自己的理解，首先%%% ysy。

对于s，t，我们先求出lca（我用的是树链剖分）。

s，t对答案贡献：

当在x->lca

dep[i]+t[i]=dep[s]

当在lca->y

dep[y]+dep[x]-2*dep[lca]=t[i]+dep[y]-dep[i]<=>t[i]-dep[i]=dep[x]-2*dep[lca]

这样我们就可以处理两个数组，一个记加的，一个记减的。

但是当然还有问题，有可能预处理在x打了标记，可实际这条路没有经过i，结果在i的答案加了怎么办？

注意，每次的x，y，在处理完lca就没有用了，所以多搞一个减去这些的操作，消除对子树以外的影响，但也有可能在子树内对其他无用的节点产生影响，所以要在dfs到s，t时，把影响减掉。

还有数组要开大点啊，我也不知道为什么一开始觉得够了还RE…

这题真的折磨死蒟蒻了。

代码：

 //2017.11.3
 //lca
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 inline int read();
 namespace lys{
      ;
     struct edge{
         int to;
         int next;
     }e[N*];
     ];
     ],p1[N],p2[N],n1[N*],n2[N*];
     ],y[N<<],t[N],ans[N],pre[N];
     int son[N],siz[N],dep[N],top[N],fa[N];
     int n,m,cnt;
     void add(int x,int y){
         e[++cnt].to=y;e[cnt].next=pre[x];pre[x]=cnt;
         e[++cnt].to=x;e[cnt].next=pre[y];pre[y]=cnt;
     }
     void dfs1(int node,int deep){
         dep[node]=deep;
         siz[node]=;
         int i,v;
         for(i=pre[node];i;i=e[i].next){
             v=e[i].to;
             if(v==fa[node]) continue ;
             fa[v]=node;
             dfs1(v,deep+);
             siz[node]+=siz[v];
             if(siz[son[node]]<siz[v]) son[node]=v;
         }
     }
     void dfs2(int node,int tp){
         top[node]=tp;
         if(!son[node]) return ;
         dfs2(son[node],tp);
         int i,v;
         for(i=pre[node];i;i=e[i].next){
             v=e[i].to;
             if(v==fa[node]||v==son[node]) continue ;
             dfs2(v,v);
         }
     }
     int lca(int x,int y){
         int f1,f2;
         while(true){
             f1=top[x],f2=top[y];
             if(f1==f2) return dep[x]<dep[y]?x:y;
             if(dep[f1]>dep[f2]) x=fa[f1];
             else y=fa[f2];
         }
     }
     void init(bool flag,bool up,int node,int deep){
         sig[++cnt]=up;
         w[cnt]=deep;
         if(flag){
             n1[cnt]=p1[node];
             p1[node]=cnt;
         }
         else{
             n2[cnt]=p2[node];
             p2[node]=cnt;
         }
     }
     void dfs(int node){
         int i,v;
         for(i=p1[node];i;i=n1[i])
             if(sig[i]) x[w[i]]++;
             else y[w[i]+n]++;
         ans[node]+=x[t[node]+dep[node]]+y[t[node]-dep[node]+n];
         for(i=p2[node];i;i=n2[i])
             if(sig[i]) x[w[i]]--;
             else y[w[i]+n]--;
         for(i=pre[node];i;i=e[i].next){
             v=e[i].to;
             if(v==fa[node]) continue ;
             dfs(v);
         }
         ans[node]-=x[t[node]+dep[node]]+y[t[node]-dep[node]+n];
     }
     int main(){
         int i,u,v,x;
         n=read(); m=read();
         ;i<n;i++){
             u=read(); v=read();
             add(u,v);
         }
         dfs1(,),dfs2(,);
         ;i<=n;i++) t[i]=read();
         ;i<=m;i++){
             u=read(); v=read();
             x=lca(u,v);
             init(,,x,dep[u]);
             init(,,x,dep[u]-(dep[x]<<));
             init(,,u,dep[u]);
             init(,,v,dep[u]-(dep[x]<<));
             if(t[x]==dep[u]-dep[x]) ans[x]--;
         }
         dfs();
         ;i<=n;i++) printf("%d ",ans[i]);
         puts("");
     }
 }
 int main(){
     lys::main();
     ;
 }
 inline int read(){
     ,ff=;
     char c=getchar();
     '){
         ;
         c=getchar();
     }
     +c-',c=getchar();
     return kk*ff;
 }