（转网上的图）

(原文地址 ,http://www.cnblogs.com/knowledgesea/p/5296008.html)

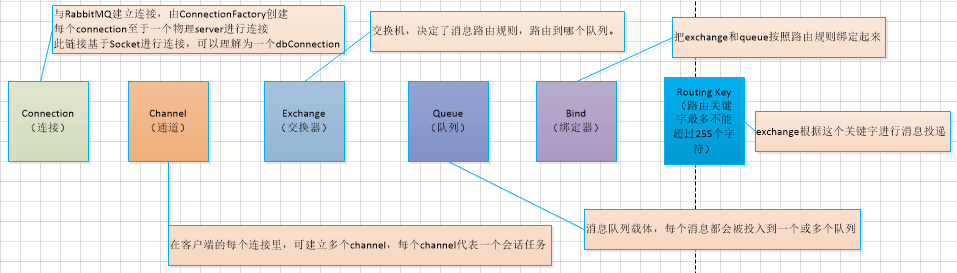
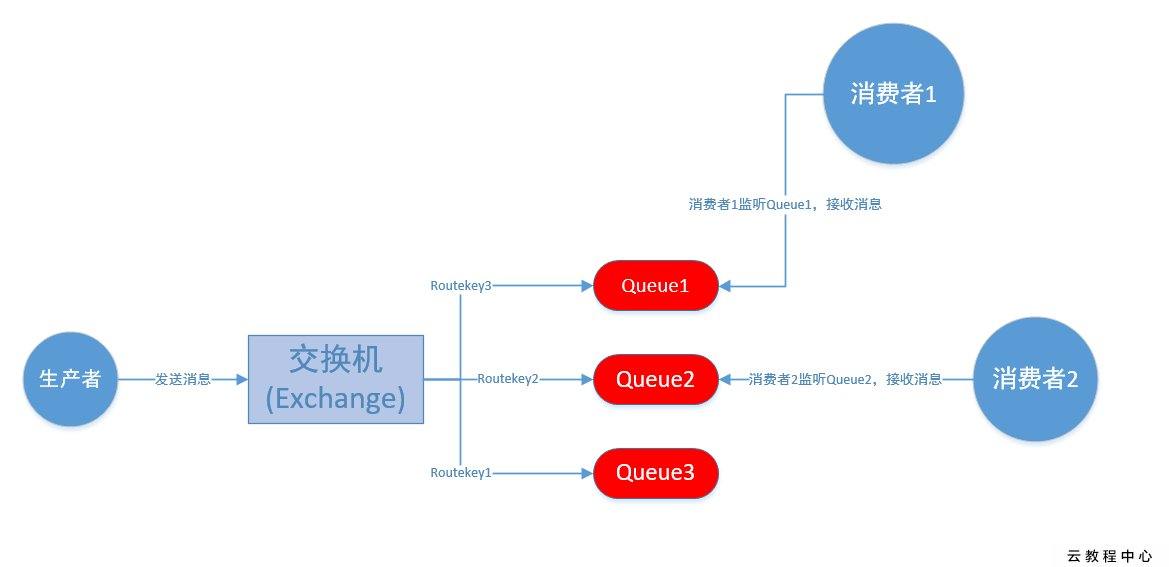
RabbitMQ 工作图解的更多相关文章

  1. RabbitMQ系列（二）深入了解RabbitMQ工作原理及简单使用

    深入了解RabbitMQ工作原理及简单使用 RabbitMQ系列文章 RabbitMQ在Ubuntu上的环境搭建 深入了解RabbitMQ工作原理及简单使用 RabbitMQ交换器Exchange介绍 ...

  2. 深入解读RabbitMQ工作原理及简单使用

    RabbitMQ系列目录 RabbitMQ在Ubuntu上的环境搭建 深入解读RabbitMQ工作原理及简单使用 Rabbit的几种工作模式介绍与实践 Rabbit事务与消息确认 Rabbit集群搭建 ...

  3. 深入了解RabbitMQ工作原理及简单使用

    深入了解RabbitMQ工作原理及简单使用 RabbitMQ系列文章 RabbitMQ在Ubuntu上的环境搭建 深入了解RabbitMQ工作原理及简单使用 RabbitMQ交换器Exchange介绍 ...

  4. 1.RabbitMQ工作模型与基本原理

        1.了解 MQ 的本质和 RabbitMQ 的特性: 2.掌握 RabbitMQ 的 Java API 编程和 Spring 集成 RabbitMQ 1. MQ 了解 1.1. 消息队列简介 ...

  5. RabbitMQ工作模式

    ------------恢复内容开始------------ RabbitMQ基本概念: Producer:生产者(消息的提供者) Consumer:消费者(消息的使用者) Message:消息(程序 ...

  6. RabbitMQ入门及其几种工作模式

    1.简介 MQ全程Message Queue,用于应用程序和应用程序间进行通信.RabbitMQ采用Erlang编写,实现了AMQP(高级消息队列)协议,跨平台,支持各种主流的操作系统和多种客户端. ...

  7. 面试官：RabbitMQ有哪些工作模式？

    哈喽!大家好,我是小奇,一位不靠谱的程序员 小奇打算以轻松幽默的对话方式来分享一些技术,如果你觉得通过小奇的文章学到了东西,那就给小奇一个赞吧 文章持续更新 一.前言 今天又.又.又来面试了,还是老规 ...

  8. [Open Source] RabbitMQ 高可用集群方案

    简介 RabbitMQ是用erlang开发的,集群非常方便,因为erlang天生就是一门分布式语言,但其本身并不支持负载均衡. Rabbit模式大概分为以下三种:单一模式.普通模式.镜像模式 Rabb ...

  9. 云计算openstack共享组件（3）——消息队列rabbitmq

    队列(MQ)概念: MQ 全称为 Message Queue, 消息队列( MQ ) 是一种应用程序对应用程序的通信方法.应用程序通过读写出入队列的消息(针对应用程序的数据)来通信,而无需专用连接来链 ...

随机推荐

  1. kafka学习(四)

    集群成员关系 kafka使用Zookeeper 来维护集群成员的信息.每个broker都有一个唯一标识符,这个标识符可以在配置里指定,也可以自动生成.在broker启动的时候,它通过创建临时节点把自己 ...

  2. vue项目中，无需打包而动态更改背景图以及标题

    1.背景 今天,项目经理对已完成的项目提出了一个需求,即项目的基础功能目前针对于各个基层法院都适用,而对于不同的法院,我们每次都需要前端研发来更改所属法院的法院名称以及背景图,这样对于演示者来说是非常 ...

  3. SpringBoot 使用JPA+MySQL+Thymeleaf 总结 二

    SpringBoot 使用JPA+MySQL+Thymeleaf 总结 一 SpringBoot 使用JPA+MySQL+Thymeleaf 总结 二 方法一 使用原生sql查询 或者 为方法名增加 ...

  4. Java 多线程编程之：notify 和 wait 用法

    wait 和 notify 简介 wait 和 notify 均为 Object 的方法: Object.wait() —— 暂停一个线程 Object.notify() —— 唤醒一个线程 从以上的 ...

  5. 剑指offer-二叉树的镜像-python

    题目描述 操作给定的二叉树,将其变换为源二叉树的镜像. 输入描述: 二叉树的镜像定义:源二叉树 8 / \ 6 10 / \ / \ 5 7 9 11 镜像二叉树 8 / \ 10 6 / \ / \ ...

  6. egg框架实现表单验证及获取验证的错误信息

    最近再看egg框架 是阿里今年开源的一款基于nodejs的mvc架构的web框架 感兴趣的同学可以看看 因为之前一直做php的关系 在tp,yii,laravel这些框架中对于前台发送的数据,模型里都 ...

  7. js随机验证码

    随机验证码: <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <ti ...

  8. php 爬虫爱奇艺 视频、内容

    ,][];   ][];   ][]);   ][]);   ]);    ][]; ][]; ][])) {     ][];   }][])) {     ][];   }   ][];   ; ...

  9. idea解除版本控制

    解除版本控制删除两个文件: 1.idea中删除vcs.xml 2.在项目文件夹中删除.git 参考:https://blog.csdn.net/qq_37999340/article/details/ ...

  10. Ubuntu 14.04 下的MAC OS X 主题安装

    Ubuntu 14.04 下的MAC OS X 主题安装 安装 MAC OS X 主题会帮助你的 Ubuntu 14.04 看起来更像MAC OS X.在这里我们介绍的Macbuntu安装包包含了GT ...