[CSP-S模拟测试]:画作（BFS+数学）

题目描述

小$G$的喜欢作画，尤其喜欢仅使用黑白两色作画.
画作可以抽象成一个$r\times c$大小的$01$矩阵。现在小$G$构思好了了他的画作，准备动笔开始作画。初始时画布是全白的，他每一次下笔可以将一个四联通的部分涂成黑色或白色。
你需要告诉他，在给出的构思下，他最少需要下笔多少次才能完成画作。

---

输入格式

第一行两个正整数$r,c$。
接下来$r$行，每行$c$个字符，表示目标画作。

---

输出格式

输出一行一个正整数，表示最少需要的下笔步数。

---

样例

样例输入：

3 3
010
101
010

样例输出：

2

---

数据范围与提示

$\bullet Subtask\ 1(19pts):r\times c\leqslant 15$。
$\bullet Subtask\ 2(7pts):r=1$。
$\bullet Subtask\ 3(25pts):r,c\leqslant 30$。
$\bullet Subtask\ 4(49pts):r,c\leqslant 50$。

---

题解

又是一道看完一脸懵的题。

先来解释一下题意，好像好多人不知道什么是四联通。

那么什么是四联通，我们可以感性的将其理解为有边相邻的两个联通块，如下图：

再举一个不是四联通的例子，如下图中，两个联通块只是有定点相邻，但是没有边相邻，所以不是四联通：

而对于这道题，样例中两步是怎么走出来的？

首先，一开始是一片白：

然后我们将其染成下图：

在将中间染白即可：

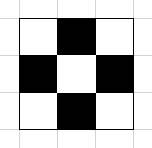
一共两步，刚刚好。

下面来看怎么找答案。

考试的时候想了一种思路，从外面往里一层一层收缩，然后我也就陷进去了，到死都没有想出来。

瓶颈就在于第一次收缩如何统计答案，有兴趣的人可以私信我。

一个比较显然的结论：存在一种最优方案使得每次操作的区域是上一次的子集且颜色与上一次相反。

这个仔细脑补一下就好了，下面我也给出官方题解中的证明：

记$S$为当前所有操作区域的并，$T$为接下来一步的操作区域，我们有：
$1.$与$S$有交的情况一定可以转化成$T$被$S$包含的情况。
$2.T$与$S$交集为空时，可以找一个连接$S$和$T$的集合$M$并操作$S\cup T\cup M$，并将之前的所有操作连接到更外的层以及外层的连接部分同时操作，特殊处理最外层和第二层的情况。
$3.T$被$S$包含时，$T$落在某个完整区域内时等价于情况二，否则一定连接若干个同色块，这些块可以同时处理，步数一定不会更劣。

显然我们不能直接从外面往里面缩，所以我们考虑从中间往外面扩。

枚举扩的起点，然后用如上性质往外扩，对于所有的点取最小值即可。

使用双端队列即可优化成$\Theta(n^4)$。

时间复杂度：$\Theta(n^4)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int r,c;
char ch[100];
bool Map[100][100];
int dis[100][100];
int ans=1<<30;
deque<pair<int,int> > q;
int fx[4][2]={{1,0},{0,1},{0,-1},{-1,0}};
bool check(int u,int v){return u>=1&&u<=r&&v>=1&&v<=c;}
int main()
{
	scanf("%d%d",&r,&c);
	for(int i=1;i<=r;i++)
	{
		scanf("%s",ch+1);
		for(int j=1;j<=c;j++)
			Map[i][j]=ch[j]-'0';
	}
	for(int i=1;i<=r;i++)
		for(int j=1;j<=c;j++)
		{
			memset(dis,-1,sizeof(dis));
			int res=-1;
			dis[i][j]=0;
			q.push_back(make_pair(i,j));
			while(q.size())
			{
				pair<int,int> flag=q.front();
				q.pop_front();
				int x=flag.first;
				int y=flag.second;
				if(Map[x][y])res=max(res,dis[x][y]);
				for(int k=0,u,v;k<4;k++)
					if(check(u=x+fx[k][0],v=y+fx[k][1])&&dis[u][v]==-1)
					{
						if(Map[x][y]==Map[u][v])
						{
							dis[u][v]=dis[x][y];
							q.push_front(make_pair(u,v));
						}
						else
						{
							dis[u][v]=dis[x][y]+1;
							q.push_back(make_pair(u,v));
						}
					}
			}
			ans=min(ans,res+1);
		}
	printf("%d",ans);
	return 0;
}

---

rp++