【leetcode】883. Projection Area of 3D Shapes

题目如下：

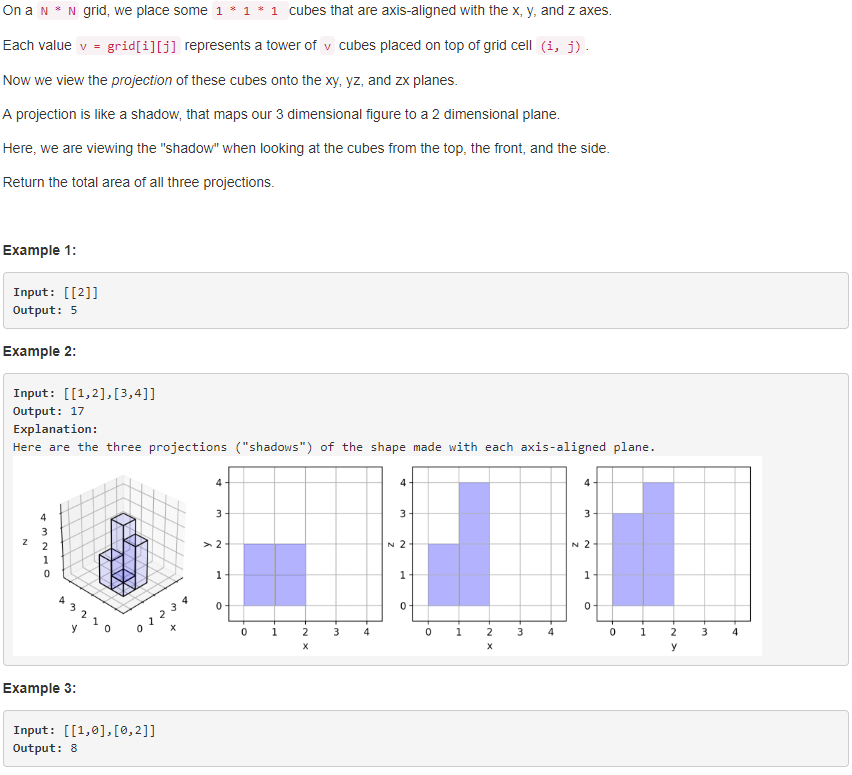
解题思路：分别求出所有立方体的个数，各行的最大值之和，各列的最大值之和。三者相加即为答案。

代码如下：

class Solution(object):
    def projectionArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        front = [0] * len(grid)
        side = [0] * len(grid)
        top = 0
        for i in range(len(grid)):
            for j in range(len(grid[i])):
                if grid[i][j] == 0:
                    continue
                top += 1
                front[i] = max(front[i],grid[i][j])
                side[j] = max(side[j],grid[i][j])
        return top + sum(front) + sum(side)