Python算法每日一题--002--求众数
给定一个大小为 n 的数组,找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在众数。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/majority-element
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
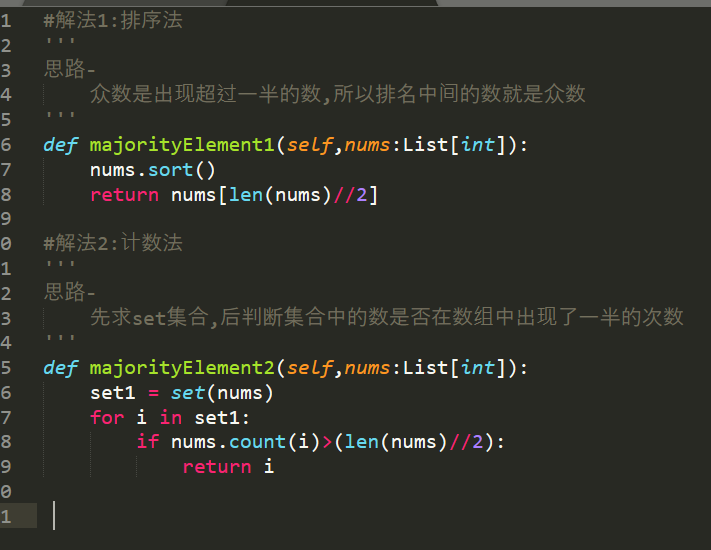
Python算法每日一题--002--求众数的更多相关文章
- Python:每日一题002
题目: 企业发放的奖金根据利润提成.利润(I)低于或等于10万元时,奖金可提10%:利润高于10万元,低于20万元时,低于10万元的部分按10%提成,高于10万元的部分,可提成7.5%:20万到40万 ...
- Python算法每日一题--001--给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次.找出那个只出现了一次的元素. 说明: 你的算法应该具有线性时间复杂度. 你可以不使用额外空间来实现吗? 示例 1: 输入: [ ...
- Python每日一题 002
做为 Apple Store App 独立开发者,你要搞限时促销,为你的应用生成激活码(或者优惠券),使用 Python 如何生成 200 个激活码(或者优惠券)? 在此生成由数字,字母组成的20位字 ...
- leecode第一百六十九题(求众数)
class Solution { public: void quick_sort(vector<int>& nums,int res,int res_end) { )//错过,不能 ...
- Python:每日一题008
题目: 判断101-200之间有多少个素数,并输出所有素数. 程序分析: 判断素数的方法:用一个数分别去除2到sqrt(这个数),如果能被整除,则表明此数不是素数,反之是素数. 个人思路及代码: li ...
- Python:每日一题007
题目: 输出 9*9 乘法口诀表. 程序分析: 分行与列考虑,共9行9列,i控制行,j控制列. 个人思路及代码: 第一版: for i in range(1,10): for j in range(1 ...
- Python:每日一题006
题目:斐波那契数列. 程序分析:斐波那契数列(Fibonacci sequence),又称黄金分割数列,指的是这样一个数列:0.1.1.2.3.5.8.13.21.34.…… 个人思路及代码: # 方 ...
- Python:每日一题005
题目: 输入三个整数x,y,z,请把这三个数由小到大输出. 程序分析: 我们想办法把最小的数放到x上,先将x与y进行比较,如果x>y则将x与y的值进行交换,然后再用x与z进行比较,如果x> ...
- Python:每日一题004
题目: 输入某年某月某日,判断这一天是这一年的第几天? 程序分析: 以3月5日为例,应该先把前两个月的加起来,然后再加上5天即本年的第几天,特殊情况,闰年且输入月份大于2时需考虑多加一天 个人的思路及 ...
随机推荐
- 如何在Web工程中实现任务计划调度
转载自: http://www.oschina.net/question/146385_37793?sort=time 下面就Servlet侦听器结合Java定时器来讲述整个实现过程.要运用Servl ...
- 问题 E: Jack的A+B
问题 E: Jack的A+B 时间限制: 1 Sec 内存限制: 128 MB提交: 1996 解决: 601[提交] [状态] [命题人:jsu_admin] 题目描述 现在有整数a,b,请按西 ...
- 性能分析之profiling及火焰图
profiling 是一项非常重要的,但又对很多程序员陌生的技术,它尤其对性能调优有显著帮助.本文以Brendan对perf的介绍稍加引入[底层涉及了太多细节,目前仅关心如何用它对服务器应用进行use ...
- 使用JS增加标签
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- jquery点击按钮弹出图片
<!DOCTYPE html><html lang="en"><head> <meta charset="UTF-8" ...
- STS插件创建springboot项目,pom第一行报unkown错误
Description Resource Path Location TypeUnknown pom.xml /amq-provider line 1 ...
- jpype测试报错,找不到类raise _RUNTIMEEXCEPTION.PYEXC("Class %s not found" % name)
最近用jpype测试java代码 公司电脑跑着没有问题,家里电脑怎么也不行,python,jdk版本啥的都一样,但总是报找不到类名的错误 raise _RUNTIMEEXCEPTION.PYEXC(& ...
- Less 混合(mixin)
Less的混合:混合可以将一个定义好的class A轻松的引入到另一个class B中,从而简单实现class B继承class A中的所有属性.我们还可以带参数地调用,就像使用函数一样. .bord ...
- [php] phar
build.php打包www目录: <?php class A{ public $a = 1; } $p = new Phar('test.phar',0,'test.phar'); $p-&g ...
- Linux中的sshd服务
Linux中的sshd服务,主要用于pst终端,远程连接到linux服务中 看sshd服务状态 service sshd status 停止sshd服务 service sshd stop 启动ssh ...
