最长公共子序列的C++实现---附二维指针的使用方法

想了挺久到底第一篇在这儿的博客写什么好，刚好这两天又一次看到动态规划的LCS算法觉得还是有点意思的，就拿来写了写，第一篇博客就发它吧。

#include<iostream>
#include<iomanip>
using namespace std;
//tag标志，0为左斜上，1取左，2取上;count为最长公共子序列计数
//计算最长公共子序列长度
void LCS_Length(char *X, char *Y, int *count[],int *tag[],int length_X, int length_Y)
{
    //第一排第一列全部是0
    for (int i = ; i < length_X+; i++)
    {
        count[i][] = ;
    }
    for (int i = ; i < length_Y+; i++)
    {
        count[][i] = ;
    }

    for (int i = ; i <= length_X; i++)
    {
        for (int j = ; j <= length_Y; j++)
        {
            if (X[i-] == Y[j - ])
            {
                count[i][j] = count[i-][j-]+;
                tag[i][j] = ;
            }
            //否则取较大的值
            else if(count[i-][j] > count[i][j-])
            {
                count[i][j] = count[i-][j];
                tag[i][j] = ;
            }
            else
            {
                count[i][j] = count[i][j-];
                tag[i][j] = ;
            }
        }
    }
}
//打印最长公共子序列元素
void Print_LCS(int *tag[],char *X,int Length_X, int Length_Y)
{
    if (Length_X ==  || Length_Y == )
    {
        return ;
    }
    int i = Length_X, j = Length_Y;
    if (tag[i][j] == )
    {
        cout<<X[i-]<<setw();
        Print_LCS(tag,X,i-,j-);
    }
    else if(tag[i][j] == )
    {
        Print_LCS(tag,X,i-,j);
    }
    else
    {
        Print_LCS(tag,X,i,j-);
    }
}

int main()
{
    //先人为设置两个序列
    char *X = "BDCABA";
    char *Y = "ABCBDA";
    int *count[];
    for (int i = ; i < ; i++)
    {
        count[i] = new int[];       //因为第一行第一列全为0，所以总共七行七列
    }
    int *tag[];
    for (int i = ; i < ; i++)
    {
        tag[i] = new int[];
    }
    LCS_Length(X,Y,count,tag,strlen(X),strlen(Y));
    cout<<"最大子序列数为"<<count[][]<<endl;
    /****************************************
    for(int i= 0; i <7; i++)
    {
        for (int j = 0; j < 7; j++)
        {
            cout<<count[i][j]<<setw(3);
        }
        cout<<endl;
    }
    *****************************************/
    Print_LCS(tag,X,strlen(X),strlen(Y));
    cout<<endl;
    return ;
}

　　主要函数有两个，一个函数是做出保存最长公共子序列的元素个数的矩阵，这里给出的示例中，两个字符串都各6个字符，所以给出的是7行7列矩阵（第一行第一列全为零）。

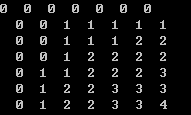
另外一个函数即为打印函数，从矩阵右下角一位开始遍历到[0][0]位，凡是遇到tag[i][j]标志为0则将该位的字符打印出来。算法比较简单易懂，具体可以参考《算法导论》。

下面补充说一个问题：二维指针到底怎么用。比如前面的二维数组初始化，如果我希望能够通过字符串的长度来给我的二维数组定义大小，而不是用常数来指定，使得我们可以通过strlen()函数来定义长度，那么就要用到二维指针。

注意：int *Arr[strlen(str)];这种声明方式是不正确的，编译器会提示错误，数组的声明必须使用常量。下面给出正确的示例：

        /***********************************************
    //华丽丽的分割线--------------------------------
    二维指针到底怎么用
    int *(*ptr) = new int*[strlen(X)];
    for (int i = 0; i < strlen(X); i++)
    {
        ptr[i] = new int[strlen(X)];
    }
    ptr[2][3] = 0;
    cout<<ptr[2][3]<<endl;
    **********************************************/