poj1840

Eqs

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 15133		Accepted: 7426

Description

Consider equations having the following form:
a1x1³+ a2x2³+ a3x3³+ a4x4³+
a5x5³=0
The coefficients are given integers from the interval
[-50,50].
It is consider a solution a system (x1, x2, x3, x4, x5) that
verifies the equation, xi∈[-50,50], xi != 0, any i∈{1,2,3,4,5}.

Determine how many solutions satisfy the given equation.

Input

The only line of input contains the 5 coefficients a1,
a2, a3, a4, a5, separated by blanks.

Output

The output will contain on the first line the number
of the solutions for the given equation.

Sample Input

37 29 41 43 47

Sample Output

654

Source

Romania OI 2002

解题思路：

直观的思路：暴力枚举，O(n^5)

题目Time Limit=5000ms，1ms大约可以执行1000条语句，那么5000ms最多执行500W次

每个变量都有100种可能值，那么暴力枚举，5层循环，就是要执行100^5=100E次，等着TLE吧。。。。

要AC这题，就要对方程做一个变形

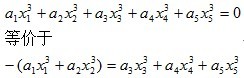
即先枚举x1和x2的组合，把所有出现过的 左值 记录打表，然后再枚举x3 x4 x5的组合得到的 右值，如果某个右值等于已经出现的左值，那么我们就得到了一个解

时间复杂度从 O(n^5)降低到 O(n^2+n^3)，大约执行100W次

我们先定义一个映射数组hash[]，初始化为0

对于方程左边，当x1=m  ,  x2= n时得到sum，则把用hash[]记录sum : hash[sum]++，表示sum这个值出现了1次

之所以是记录“次数”，而不是记录“是否已出现”，

是因为我们不能保证函数的映射为 1对1 映射，更多的是存在 多对1映射。

例如当 a1=a2时，x1=m  ,  x2= n我们得到了sum，但x1=n  ,  x2= m时我们也会得到sum，但是我们说这两个是不同的解，这就是 多对1 的情况了，如果单纯记录sum是否出现过，则会使得 解的个数 减少。

其次，为了使得 搜索sum是否出现 的操作为o(1)，我们把sum作为下标，那么hash数组的上界就取决于a1 a2 x1 x2的组合，四个量的极端值均为50

因此上界为 50*50^3+50*50^3=12500000，由于sum也可能为负数，因此我们对hash[]的上界进行扩展，扩展到25000000，当sum<0时，我们令sum+=25000000存储到hash[]

由于数组很大，必须使用全局定义

同时由于数组很大，用int定义必然会MLE，因此要用char或者short定义数组，推荐short

#include<cstdio>
#include<cstring>
using namespace std;
#define N 25000000
#define t 50
int a1,a2,a3,a4,a5;
short hash[N+];
int main(){
    while(scanf("%d%d%d%d%d",&a1,&a2,&a3,&a4,&a5)==){
        memset(hash,,sizeof hash);
        for(int x1=-t;x1<=t;x1++){
            if(!x1) continue;
            for(int x2=-t;x2<=t;x2++){
                if(!x2) continue;
                int sum=(a1*x1*x1*x1+a2*x2*x2*x2)*(-);
                if(sum<) sum+=N;
                hash[sum]++;
            }
        }
        int ans=;
        for(int x3=-t;x3<=t;x3++){
            if(!x3) continue;
            for(int x4=-t;x4<=t;x4++){
                if(!x4) continue;
                for(int x5=-t;x5<=t;x5++){
                    if(!x5) continue;
                    int sum=(a3*x3*x3*x3+a4*x4*x4*x4+a5*x5*x5*x5);
                    if(sum<) sum+=N;
                    if(hash[sum])
                    ans+=hash[sum];
                }
            }
        }
        printf("%d\n",ans);
    }
    return ;
}